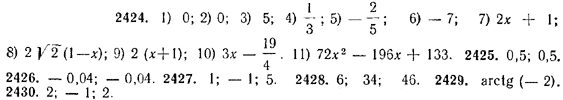11 ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЕ К ИССЛЕДОВАНИЮ ФУНКЦИЙ

§ 43. ДИФФЕРЕНЦИРОВАНИЕ ПО ФОРМУЛАМ

Производная суммы и произведения двух функций .

2422. Пользуясь определением производной, показать, что:
1) производная функции f(х) = С, принимающей постоянное значение, равна нулю; 2) производная функции f(х) =х, каждое значение которой равно значению аргумента, равна единице;
3) производная линейной функции f(х) =ах + bравна коэффициенту при независимой переменной.
Как согласуются эти выводы с геометрическим смыслом производной? с ее механическим истолкованием?

2423. 1) Сформулировать теоремы о производной суммы и производной произведения двух дифференцируемых функций. Каким приемом надо воспользоваться, чтобы распространить эти теоремы на случай любого конечного числа функций — слагаемых (сомножителей)?
2) Чему равна производная произведения двух функций, если значение одной из них постоянно во всей области ее определения?

2424. Найти производные следующих функций:

2425. Дано: f (х) = ^x/₂ + 2. Найти  f '(0); f '(— 1).

2426. Дано:  Найти F' (1); F'(— 0,1).

2427. Дано: φ (х) = (х — 1) • (х + 2). Найти φ'(0); φ'(— 1); φ' (2).

2428. Дано: ψ {х) = х (1 + 2х) (2 + 3х). Найти ψ ' (—1); ψ '(1); ψ ' (—2).

2429. Найти угол наклона касательной к кривой у = (х + 1) (х —3) в точке пересечения ее с осью ординат.

2430. Найти угловые коэффициенты касательных к кривой

у = (х — 1) • (х — 2) • (х — 3)

в точках ее пересечения с осью абсцисс.

2431. Написать уравнения касательных к кривой у = (1 + 0,5x) (1— х) в точках пересечения ее с осью абсцисс.

ОТВЕТЫ