11 ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЕ К ИССЛЕДОВАНИЮ ФУНКЦИЙ

§ 44. ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ К ИССЛЕДОВАНИЮ ФУНКЦИЙ

Максимум и минимум функции

2490. Если данная функция имеет несколько экстремумов (больше двух), может ли случиться, что какой—нибудь максимум окажется меньше минимума?

2491. Сформулировать необходимые признаки для существования максимума и минимума функции и привести геометрическую иллюстрацию в каждом случае. Может ли функция иметь максимум или минимум в точке, где производная существует и отлична от нуля?

2492. 1) Во всех ли точках, где производная равна нулю, функция имеет максимум или минимум? Ответ подтвердить примерами.
2) Сформулировать правило для нахождения максимума и минимума функции с помощью первой производной.

Исследовать на максимум и минимум с помощью первой производной следующие функции:

2493. 1) у = 2x² — 4х + 7;                              2) у = — x²_/2 — 3х + 5;
          3) y = x³_/3 + 2x²—5x + 4;                      4) y = x² — x⁴_/2.

2494.  1) y = x + ⁹/_x;                                    2) y = ^x/₂ + ²/_x;
           3) у = а + (b — x)³;                          4)  у = ^x/_a + ^a/_x,  а > 0.

2495. 1) у = (х— 1)³ • (х — 2)²;                2) у = sin x + cos x;
          3) у = sin x — х;                               4) у = sin 2x — x,         —^π/₂ < x < ^π/₂.

2496. Доказать, что следующие функции не имеют ни максимума, ни минимума:

1) у = ¹/₃ x³ — x² + x—2;           2) у = 6x⁵ —15x⁴ + 10x³

2497. 1) Доказать, что если функция  f (х) в некотором промежутке принимает только положительные значения, то максимум (или минимум) этой функции в рассматриваемом промежутке является одновременно максимумом (или минимумом) функции [f (х)]².

2) Исследовать на максимум и минимум функцию f (х) = √2 + х²  .

2498. 1) Доказать, что произведение двух положительных чисел, сумма которых постоянна, имеет максимум при равенстве множителей.

2) Доказать, что сумма двух положительных чисел, произведение которых постоянно, имеет минимум при равенстве слагаемых.

2499. Каковы должны быть коэффициенты р и q трехчлена x²  + px + q , чтобы этот трехчлен при х = 5 имел минимум, равный 1?

2500. Требуется огородить проволочной сеткой длиной а м прямоугольный участок, прилегающий к стене (рис. 72).

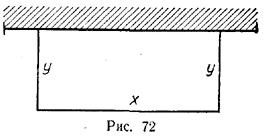
Найти размеры участка, при которых его площадь будет наибольшей.

2501. Известно, что прочность балки прямоугольного поперечного сечения пропорциональна произведению ширины на квадрат высоты сечения. Найти размеры сечения балки наибольшей прочности, которую можно выпилить из круглого бревна, имеющего наименьший диаметр в d см.

2502. Из квадратного листа жести, сторона которого равна а см, требуется сделать открытый сверху ящик возможно большей емкости, вырезая по углам равные квадраты и затем загибая края, чтобы образовать стенки ящика. Какова должна быть длина стороны вырезаемых квадратов?

2503. Материальная точка совершает прямолинейное движение по закону
s = f (t) = 5t + 2t² — ²/₃ t³, где s — путь в метрах и t — время в секундах. В какой момент времени t скорость движения точки будет наибольшей и какова величина этой наибольшей скорости?

2504. 1) Сформулировать правило нахождения экстремума функции с помощью второй производной.
2) Как установить существование экстремума в случае, когда при некотором значении аргумента и первая и вторая производные исследуемой функции обращаются в нуль?

2505. Доказать, что функция у = ax²  + bx + c  имеет только один максимум или минимум.

Исследовать на максимум и минимум с помoщью второй производной следующие функции:

2506. 1) у = 5 — 4х — х²;                         2) у = (х + 1) (х + 2);
          3) у = 36х — 3х² — 2х³;                 4) у = х² (3х² + 8х — 18).

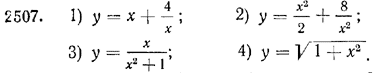
2508. 1) у = cos 2х, 0 < х < 2π;                  2) у = sin 2х + cos 2х, 0 < х < π;
          3) у = ^x/₂  — sin х, 0 < х < π;              4) у = ^x/₂  — cos х, 0 < х < 2π.

2509. 1) у = sin х • sin (х — ^π/₄),  0 < х < π;          2) у = cos х • cos (^π/₃ — х),  0 < х < π:;
         3) у = sin х • (1 — cos х), 0 < х < 2π;           4) у = sin⁴ х + cos⁴ х, 0 < х < 2π.

2510. Показать, что из всех равнобедренных треугольников, вписанных в данный круг, наибольший периметр имеет равносторонний треугольник.

2511. Из куска картона 32 см  X  20 см требуется сделать коробку без крышки наибольшей вместимости, вырезая по углам равные квадраты и затем загибая выступы для образования боков коробки. Какова должна быть длина сторон вырезаемых квадратов?

2512. Доказать, что из всех прямоугольных треугольников с заданной гипотенузой наибольшую площадь имеет равнобедренный треугольник.

2513. Сечение туннеля (или шлюзового канала) имеет форму прямоугольника, завершенного полукругом (рис. 73).

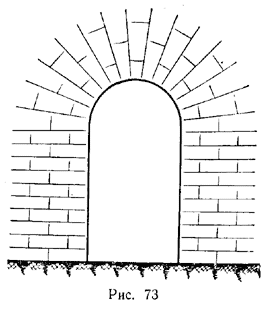
1) Зная периметр сечения 2р, определить, при каком радиусе полукруга площадь сечения будет наибольшей.

2) Зная площадь сечения S, определить, при каких условиях периметр сечения будет наименьшим.

2514. Поперечное сечение каналов в большинстве случаев имеет форму равнобедренной трапеции; часть периметра сечения канала, соприкасающаяся с водой, называется смоченным периметром, а часть сечения канала, занятая водой,—живым сечением (рис. 74).

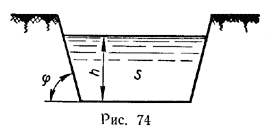
Чтобы увеличить пропускную способность канала, имеющего постоянную площадь живого сечения, при сооружении его стараются сделать смоченный периметр наименьшим. Определить, при каком угле φ откоса при заданной глубине h канала и данной площади S живого сечения канала смоченный периметр имеет наименьшее значение и какое именно.

2515. Из прямоугольного листа жести шириной 60 см требуется изготовить открытый сверху желоб, имеющий в поперечном сечении форму равнобедренной трапеции с боковой стороной 20 см. Под каким углом к дну желоба надо наклонить его стенки, чтобы вместимость желоба была наибольшей?

2516. Из всех цилиндров данного объема V найти тот, который имеет наименьшую полную поверхность.

2517. Лампа висит над центром круглого стола радиуса r. При какой высоте лампы над столом освещенность предмета, лежащего на краю стола, будет наилучшей (освещенность прямо пропорциональна косинусу угла падения лучей света и обратно пропорциональна квадрату расстояния от источника света)?

2518. Найти высоту конуса максимального объема, который можно вписать в шар радиуса R.

2519. Найти высоту цилиндра наибольшего объема, который можно вписать в данный прямой конус с высотой Н и радиусом основания R.

2520. Найти высоту цилиндра наибольшего объема, который можно вписать в шар радиуса R.

2521. Движение тела, брошенного под углом α  к горизонту с начальной скоростью v₀, имеет траекторию  При каком значении х тело достигает максимальной высоты? Вычислить наибольшую высоту подъема тела, если
α = 45°, v₀ = 400 м/сек, g = 10 м/сек².

2522. 1) Имея N одинаковых электрических элементов, можно различными способами составлять из них батареи, соединяя по п элементов последовательно, а затем полученную группу числом ( ^N/_n ) параллельно. Сила тока, даваемая такой батареей, определяется формулой

где е — электродвижущая сила одного элемента, r — его внутреннее сопротивление, R — внешнее сопротивление.

Определить, при каком значении п батарея даст ток наибольшей силы.

2) Решить задачу для случая, когда в каждой группе элементы соединены параллельно, а сами группы соединены последовательно.

Доказать неравенства:

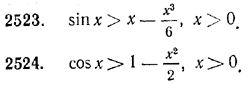
ОТВЕТЫ