1. Задачи и упражнения для повторения курса V—VIII классов

§ 2. АЛГЕБРА

Тождественные преобразования алгебраических выражений

54. Если п — натуральное число, то какие числа изображают следующие алгебраические выражения:

1) 2п; 2) 2n+1; 3) 3п; 4) 3п ± 1.

55. Доказать, что:
1) сумма двух последовательных натуральных чисел — число нечетное, а произведение их — число четное;
2) сумма двух любых нечетных чисел есть число четное, а произведение их — число нечетное;
3) произведение двух любых последовательных четных чисел делится на 8;
4) сумма любого двузначного числа и числа, изображенного теми же цифрами, но написанными в обратном порядке, делится на 11.

56. Доказать, что если к двузначному числу приписать такое же число и полученное четырехзначное число разделить на 101, то в частном получится первоначальное число.

57*. Упростить следующие выражения:

1) x + | 1 — x| + 2 — | x — 2 |, если 1 < x< 2;

2) | x| + | x+ 1| + | x— 2 | при x< 2;

3) | x—1 | + ^x/_|x|— | x+ 1 | при x> — 2.

58. Доказать тождества и привести словесные формулировки:

1) (а ± b)² = а² ± 2аb + b²;

2) (а ± b)³ = а³ ± 3а²b + 3аb²± b³ ;

3) (а + b) (а — b) = а² — b²;

4) (а ± b) (а² + ab + b²) = а³ ± b³;

59. 1) Верно ли, что (а — b)² = (b — а)²?

2) Какое выражение надо прибавить к квадрату разности двух чисел, чтобы получить квадрат суммы тех же чисел?

3) Какое выражение надо вычесть из куба суммы чисел а и b, чтобы получить сумму кубов тех же чисел?

60. Для каких значений а и bсправедливы равенства:
1) (а —b)³ = (b — а)³;
2) (а + b)² = а² + b²?

61. Могут ли квадраты двух неравных чисел быть равными между собой?

62*. Объяснить, почему квадраты двух натуральных чисел, у которых сумма последних цифр равна 10, оканчиваются одной и той же цифрой.

63. Вычислить (устно), применяя формулы сокращенного умножения:

1) 21²; 41²; 71²; 91²; 101²; 22²; 32²; 52²; 62²;

2) 19²; 29²; 59²; 99²; 98²; 48²; 58²;

3) 19 • 21; 39 • 41; 69 • 71; 89 • 91; 18 • 22; 28 • 32;

4) 47² —46²; 83² —82²; 68² — 67²; 24² — 21²; 32² — 29².

64. 1) Доказать справедливость приближенных равенств при достаточно малом х:
а) (1 ± х)² ≈1 ± 2х;
б) (1 ± х)³ ≈1 ± 3х.

В каждом случае указать абсолютную погрешность, допускаемую при пользовании этими формулами.

2) Вычислить по формулам приближения и найти абсолютную погрешность результата:
а) 1.003²; 1,0025²; 1,015²; 0,998²; 2.008²; 5,042²;
б) 0.999³; 1.002³; 1.997³.

65. 1) Доказать, что при х = а — 1 выражение х² + х + а является точным, квадратом.

2) Найти такое натуральное значение х, при котором численное значение трехчлена
х² + х + 41 окажется точным квадратом.

66. Найти числовое значение выражения:

1) а³ — b³ — 3аb (а — b) при а = —27 и b = —33;

2) а² — 32а + 260 при а = 28;

3) х³ — 3х² + 3х при x= 1, 2, 3, 4, 5, 6.

67*. Доказать, что:
1) квадрат нечетного натурального числа есть число нечетное;
2) квадрат всякого нечетного числа, уменьшенный на 1, делится на 8;
3) разность между кубом натурального числа и самим числом делится на 6;
4) сумма кубов трех последовательных натуральных чисел делится на 3;
5) квадрат натурального числа при делении на 3 дает остаток, равный 0 или 1;
6) куб натурального числа при делении на 9 дает остаток, равней 0, 1 или 8.

68. Выделить из данного трехчлена квадрат суммы (или разности) двух чисел:

1) х² + 6х + 16;
2) х² — 10х + 16;
3) х² — х + 1;
4) х² + 5х — 4.

69. Найти наименьшее численное значение выражения х²— 6х + 34.

70. При каких значениях а трехчлен 10а — 23 — а² принимает наибольшее значение? Найти это наибольшее значение трехчлена.

71. Доказать, что выражение (х — 1) (х — 3) + 1 при любых значениях х принимает неотрицательные значения.

72. В следующих примерах по двум данным величинам найти третью:

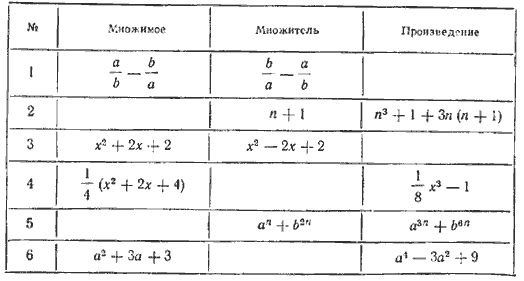
Разложить на множители:

73. 1) 18а³b² — 2аb⁴;
2) 4а² — 4b² — 4а + 1.

74. 1) 9а² — b² + 2b — 1;
2) a² + b² + 2a — 2b — 2ab.

75. 1) (a + 1) (a² —b²) —(a + b) (a² — 1);
2) (a + b) (a³ — b³) — (a — b) (a³ + b³).

76. 1) x⁴ — x² (a² + 1) + a²;
2) x³ + (a — 1) x + a.

77. 1) a⁴ — 1; 2) 8 — x⁵; 3) a⁶ + 1; 4) a⁴ + 4b⁴.

78*. 1) x²y + xy² + x²z + xz² + y²z + уz² + 2xyz;

2) x²y + xy² + x²z + xz² + y²z + yz² + 3хуz.

79*. 1) a⁴ + a² + 1; 2) x⁴ + x²y² + y⁴.

80*. Доказать, что:
1) сумма трех любых последовательных натуральных степеней числа 2 делится на 14;
2) произведение квадрата целого числа на число, предшествующее этому квадрату, всегда делится на 12;
3) при всяком нечетном значении х числовое значение выражения х³ + 3х² — х — 3 делится на 48;
4) при всяком натуральном х числовое значение выражения (х2 +3х + 1)² —1 делится на 24.

81. Доказать, что если к произведению трех последовательных натуральных чисел прибавить среднее из них, то полученная сумма будет равна кубу среднего числа.

82*. Доказать, что если а + b + с = 0, то а³ + b³ + с³ = 3аbс.

83. Сократить дроби:

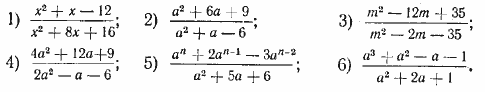
84. Найти числовые значения следующих выражений, предварительно упростив их:

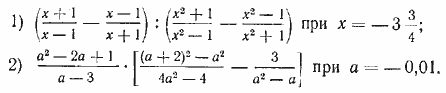
Произвести указанные действия:

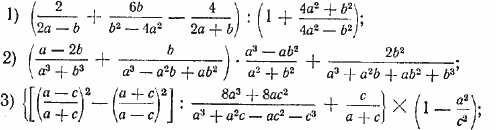
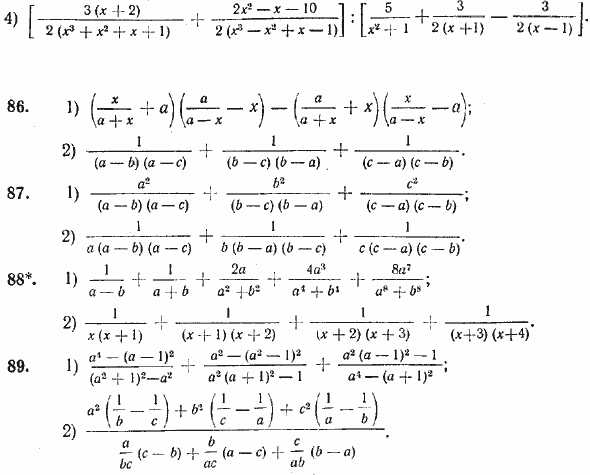
90*. Доказать, что если , то

(а + b) (а + с) (b + с) = 0.

91*. Доказать, что если ^a/_b = ^b/_c, то .

92*. Определить A и В так, чтобы имело место тождество:

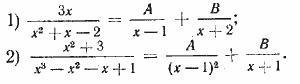
ОТВЕТЫ