5. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ЛЮБОГО АРГУМЕНТА

§ 22. ГРАФИКИ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ

Построение косинусоиды. Свойства косинуса

1097. 1) Доказать геометрически соотношение cos α = sin (α + ^π/₂ ).
Рассмотреть случаи:

а) 0 < α < ^π/₂ (рис.47);     б) ^π/₂ < α < π;    в) π < α < ^3π/₂;    г) ^3π/₂ < α < 2π.

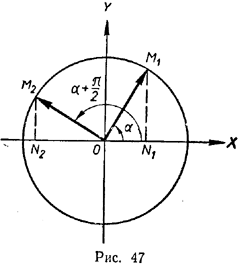
2) Исходя из доказанного соотношения, указать геометрический способ построения графика функции у = cos x.

3) Каким преобразованиям надо подвергнуть обыкновенную синусоиду, чтобы получить график функции у = cos x (косинусоиду)?

4) Имеет ли косинусоида центры и оси симметрии? Ответ обосновать на единичной окружности.

1098. Построить схематически косинусоиду на интервале [—3π; 3π] и выполнить следующие упражнения:

1) Проиллюстрировать по графику, что:

а) функция cos x не может принимать значений, превосходящих по абсолютной величине единицу, т. е. —1 < cos x < 1;

б) каждому действительному значению х соответствует только одно значение cos х (свойство однозначности косинуса);

в) при замене произвольного значения аргумента х противоположным ему значением —х значение функции не изменяется, т. е. cos (—х) = cos х (свойство четности косинуса). Подтвердить это свойство на единичной окружности. Как можно использовать свойство четности косинуса при построении его графика;

г) при изменении произвольного значения аргумента на число, кратное числу 2π, значение функции cos x не изменяется, т. е. cos (х + 2πk) = cos x (свойство периодичности косинуса). Проиллюстрировать свойство периодичности косинуса на единичной окружности. Как можно использовать периодичность косинуса при построении его графика;

д) при изменении произвольного знамения аргумента на число π значение функции у заменяется противоположным ему значением — у, т. е. cos (x ± π) = — cos x. Подтвердить это свойства на единичной окружности;

е) уравнение cos х = 0,5 имеет бесчисленное множество решений. Назвать несколько частных решений этого ypавнення;

2) Указать интервалы, в которых функция у = cos х принимает, а) положительные значения; б) отрицательные значения.  Какие четверти единичной окружности соответствуют этим интервалам.'

3)  Выделить на оси абсцисс и на единичной окружности интервалы, в которых функция у = cos x а) возрастает; б) убывает. Проиллюстрировать на графике, что в любом интервале монотонности косинус последовательно принимает все свои возможные значения, каждому из которых соответствует только одно значение аргумента в рассматриваемом интервале.

1099. По графику функции cos x (рис. 48) ответить на следующие вопросы:

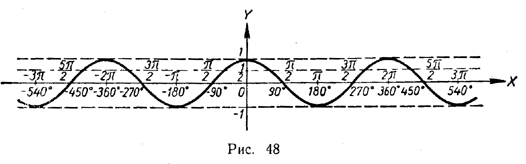
1)  Как изменяется cos x, если аргумент х:  
а) увеличивается от —2π до π; б) уменьшается от 2,5π до 1,5π?

2)  Чему равен косинус числа: а) π; б) 2π; в) —0,5π; г)  —2π?

3) Что меньше: a) cos 0,7 или cos 1;  б) cos (^π/₂ + 1) или cos ( ^π/₂ — 1)?

4)   При каких значениях х функция cos x равна:  а) 0; б)  1; в) —1?

5)  Проиллюстрировать на графике, что не существует значений аргумента х, при которых функция cos x была равна 2.