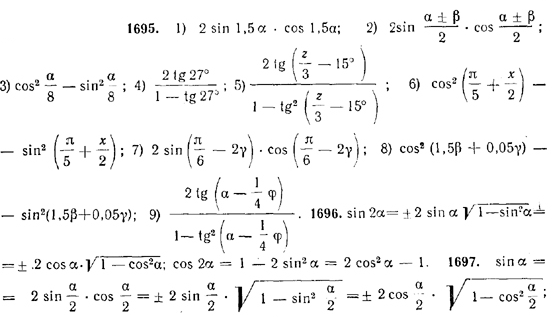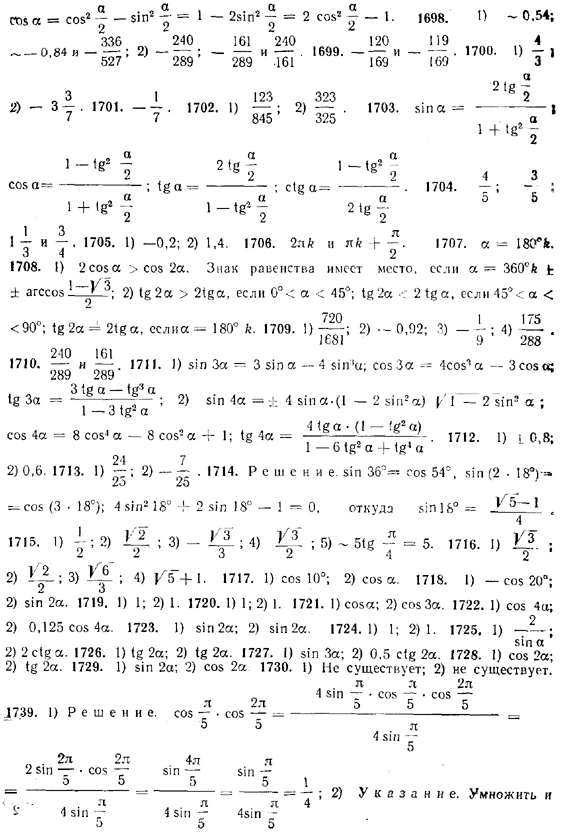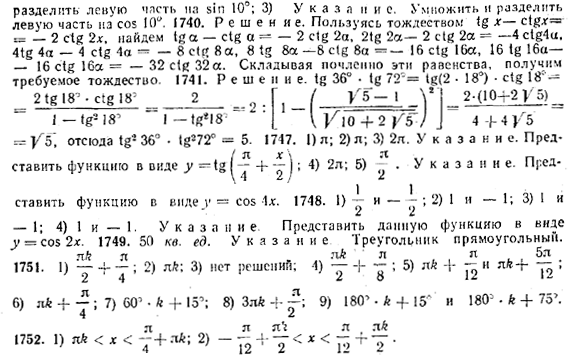8 ТРИГОНОМЕТРИЧЕСКИЕ ТЕОРЕМЫ СЛОЖЕНИЯ И ИХ СЛЕДСТВИЯ

§ 30. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
ДВОЙНОГО И ПОЛОВИННОГО АРГУМЕНТА

Функции двойного аргумента

1695. Следующие функции выразить через функции вдвое меньшего аргумента:

1) sin 3α ;                    2) sin (α  ± β);               3) cos 0,25α ;
4) tg 54°;                    5) tg ( ^2π/₃ — 30°);        6) cos ( ^2π/₅ + х);
7)sin ( ^π/₃— 4γ);         8) cos (3β + 0,1γ);         9) tg (2α — ^φ/₂).

1696. Выразить sin 2α и cos 2α:

1) только через sin α; 2) только через cos α.

1697. Выразить sin α и cos α

1) через sin ^α/₂ и cos ^α/₂;        2) только через sin ^α/₂;       3) только через cos ^α/₂.

1698. Вычислить:

1) sin 2α, cos 2α и tg 2α, если sin α = 0,96 и 0° < α < 90°;
2) sin α, cos α и tg α, если cos ^α/₂ = — ⁸/₁₇ и sin ^α/₂ > 0.

1699. Вычислить sin α и cos α, если tg ^α/₂ = — 2,4 и 90° < ^α/₂ < 135° .

1700. Дано: tg α = —2. Найти: 1) tg 2α; 2) tg 4α.

1701. Дано: tg ^φ/₆ = 0,5. Найти tg (45° — ^φ/₃).

1702. Дано: tg х = — 0,75; tg y = 2,4;    90° < х < 180°;   0° < у <90°.
Определить: 1) sin (х — 2у);     2) cos (2x + у).

1703. Пользуясь формулами двойного аргумента, выразить тригонометрические функции sin α, cos α, tg α и ctg α через tg ^α/₂.

1704. Найти sin α, cos α, tg α и ctg α, если tg ^α/₂ = 0,5.

1705. Дано: tg ^x/₂ = 3. Вычислить: 1) sin x + cos x; 2) sin x — cos x;.

1706. Уравнение sin x + cos  x = 1 решить двумя способами:
1) применяя формулы двойного аргумента;
2) выразив sin x и cos x  через tg ^x/₂.

1707. Доказать, что sin 2α < 2 sin α, если 0° < α < 90°.
Вывести условие, при котором sin 2α = 2 sin α.

1708. Известно, что 0° < α < 90°. Что больше:
1) cos 2α или 2 cos α? При каких значениях α имеет место равенство cos 2α = 2 cos α?
2) tg 2α или 2 tgα, где α =/= 45°?
При каких значениях α имеет место равенство tg 2α = 2 tg α?

1709. Вычислить:

1) sin (2 arcsin —⁴⁰/₁₁),                2) cos (2 arccos 0,2);
3) cos (2 arccos —²/₃),                 4) tg (2 arctg 0,28).

1710. В равнобедренном треугольнике синус угла при основании равен ¹⁵/₁₇; определить синус и косинус угла при вершине.

1711. Выразить соответственно через sin α, cos α и tg α:

1) sin 3α; cos 3α и tg 3α; 2) sin 4α; cos 4α и tg 4α.

1712.  Дано ^{sin 3α}/_{sin α} = 2,2.    Найти: 1) sin 2α;    2) cos 2α .

1713. Дано: ctg α = 2.    Найти: 1) sin 4α; 2) cos 4α.

1714. Вычислить (без таблиц) sin 18°.

1715. Вычислить:

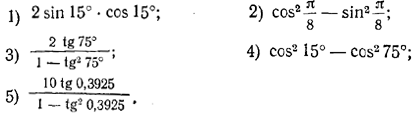
1716. Вычислить:

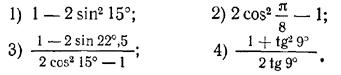
Упростить выражения.

1717. 1) 2 sin 40° • sin 50°;      2) 2 cos (^π/₄ — ^α/₂) • cos (^π/₄. + ^α/₂) .

1718. 1) (sin 10° + sin 80°) • (cos 80° — cos 10°);
2) [sin (45° + α ) — sin (45° — α )] • [cos (45° + α ) + cos (45° — α )].

1719. 1) (sin φ — cos φ)² + sin 2φ;
2) [cos (^π/₄ + 2α ) + cos (^π/₄ — 2α )]²— cos 4α .

1722. 1) 1 — 8 sin² β  • cos² β ;      2) 0,125 — cos² x + cos⁴ x.

1723. 1) tg α— (1 + cos 2α);           2) ctg α (1 — cos 2α). 1

1724. 1) 2 cos² α — cos 2α;           2) cos 2α + 2sin² α.

1725. 1) tg 0,5 α + ctg 0,5 α;          2) ctg ^α/₂ — tg^α/₂.

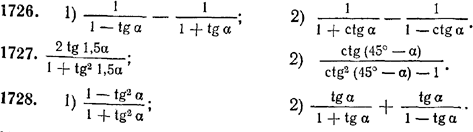
1730. Существует ли такой угол α, что:

1) sin α • cos α = sin 40°; 2) cos 2α + sin² α — 0,5 = cos 40°?

Доказать тождества.

1731. 1) cos⁴ α — sin⁴ α = cos 2α;           2) 4 sin⁴ α + sin² 2α = 4 sin² α.

1732. 1) tg 15° + ctg 15° = 4;                   2) tg 55° — tg 35°= 2 tg 20°.

1733. 1) sin 2α — tg α = cos 2α • tg α;     2) ctg α — sin 2α = cos 2α • ctg α.

1734. 1) tg α + 2 ctg 2α = ctg α;                 2) ctg α — ctg 2α = ¹/_{sin 2α},

1735.  1) ^{sin 3α}/_{sin α} —  ^{cos 3α}/_{cos α} = 2.
           2) 4 sin³ α • cos 3α + 4 cos³ α • sin 3α = 3 sin 4α.

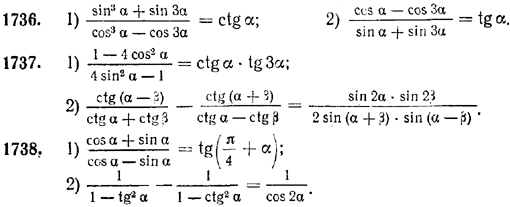
1739. 1) cos ^π/₅ • cos ^2π/₅ = 0,25;            2) 8 cos 10° • cos 20° • cos 40° = ctg 10°.
          3) 16 cos 20° • cos 40° • cos 60° • cos 80° = 1.

1740. tg α + 2 tg 2α + 4 tg 4α + 8 tg 8α + 16 tg 16α + 32 ctg 32α = ctg α.

1741*. tg² 36° • tg² 72° = 5.

Проверить справедливость равенств.

1742*. sin (2 arcsin x) = 2x √1 — x²  ,   | x | < 1.

1743*. cos (2 arccos x) = 2x² — 1, | x | < 1.

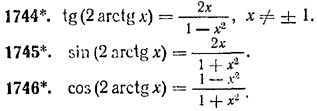
1747. Найти наименьшие положительные периоды следующих функций:

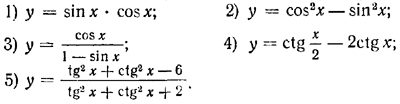
1748. Найти наибольшее и наименьшее значения функции:

1) у = sin ( x + ^π/₄) • sin (x— ^π/₄);       2)  у = sin⁴ x — cos⁴ x;

3) у = 1 —8 sin² x • cos² x;                

1749.  Середины высот треугольника лежат на одной прямой, один из его углов равен ^π/₁₂, а меньшая высота 5. Найти площадь треугольника.

1750. Доказать, что из всех прямоугольных треугольников с данной гипотенузой наибольшую площадь имеет равнобедренный треугольник.

1751. Решить уравнения:

1) 4 sin⁴ x + sin² 2x = 2;

2) sin (45° — х) • sin (45° + х) = 0,5;         3) sin х • cos x = sin 31°;

4) tg (x + ^π/₄) + tg (x— ^π/₄) = 2;                 5) ctg x — ctg 2x = 2;

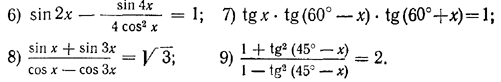
1752*. Решить неравенства:

1) tg x + ctg x + 2 ctg 2x > 2;

2) cos² у + 2 sin² 2x < 1 + ¹/₂ cos 2y.

ОТВЕТЫ