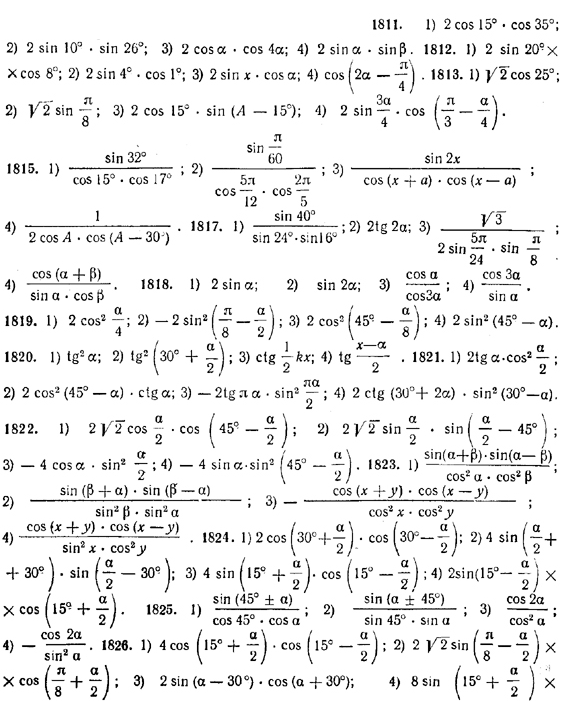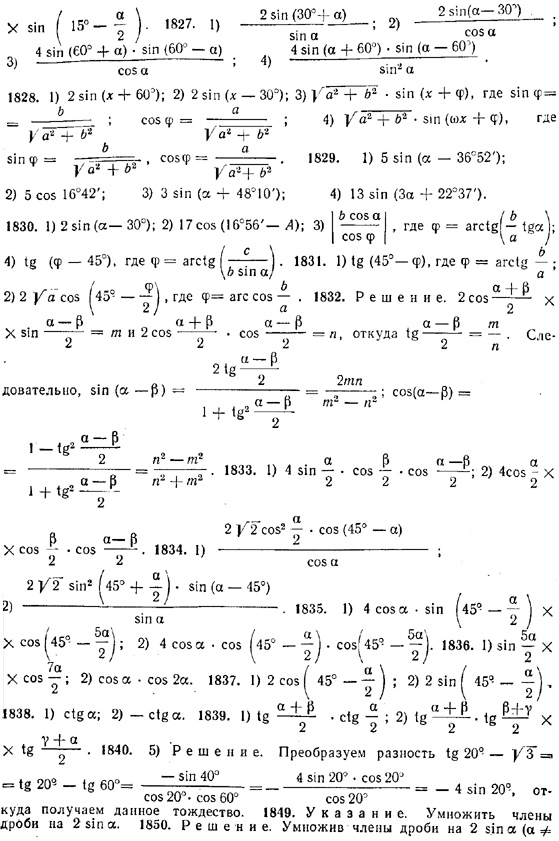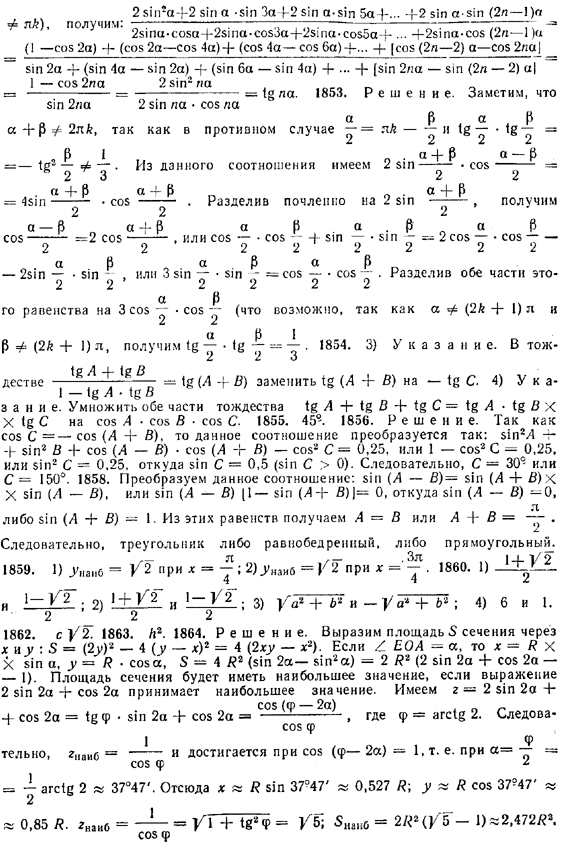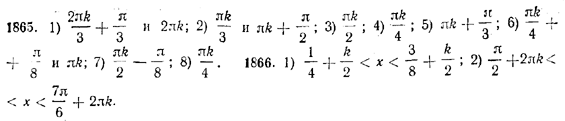8 ТРИГОНОМЕТРИЧЕСКИЕ ТЕОРЕМЫ СЛОЖЕНИЯ И ИХ СЛЕДСТВИЯ
§ 31. ПРЕОБРАЗОВАНИЕ ПРОИЗВЕДЕНИЯ
ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИИ В СУММУ;
ОБРАТНОЕ ПРЕОБРАЗОВАНИЕ
Преобразование суммы тригонометрических функций в произведение
Преобразовать в произведение.
1811. 1) cos 50° + cos 20°; 2) cos 16° — cos 36°;
3) cos 3α + cos 5α; 4) cos (α — β) — cos (α + β).
1812. 1) sin 28° + sin 12°; 2) sin 5° — sin 3°;
3) sin (x + α) + sin (x — α); 4) sin (2α — π/6) — sin (2α — π/3).
1813. 1) sin 20° +cos 20°; 2) cos π/8 — sin π/8;
3) sin A — cos (A — 60°); 4) sin (α/2+ π/3) — cos (α/2 + π/6 ).
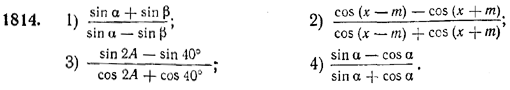
1815. 1) tg 15° + tg 17°; 2) tg 5π/12 — tg 2π/5;
3) tg (x + α) + tg (x — α); 4) tg A — tg (A — 30°).
1816. Доказать тождества:
![]()
Преобразовать в произведение:
1817. 1) ctg 24° + ctg 16°; 2) ctg (45°— α) — ctg (45° + α);
3) ctg 5π/24 + tg 3π/8; 4) ctg α — tg β.
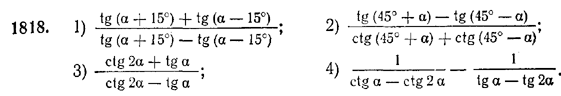
1819. 1) 1 + cos α/2; 2) cos (π/4 —α) —1;
3) 1 + sin α/4; 4) 1— sin 2α.

1821. 1) sin α + tg α; 2) cos 2α + ctg 2α;
3) sin πα — tgi πα; 4) ctg (2α + 30°) — cos (2α + 30°).
1822. 1) 1 + sin α + cos α; 2) 1 — sin α — cos α;
3) 1 — 2 cos α + cos 2α; 4) 1 — 2 sin α — cos 2α.
1823. l) tg2 α —tg2 β; 2) ctg2 α — ctg2 β;
![]()
Следующие выражения преобразовать в произведения введением вспомогательного угла:
1824. 1) 0,5 + cos α; 2) 1 — 2 cos α; 3) 1 + 2 sin α; 4) 1 — 2sin α.
1825. 1) 1 ± tg α; 2) 1 ± ctg α; 3) 1 — tg2 α; 4) 1 — ctg2 α.
1826. 1) √3 + 2 cos α; 2) 1— √2 sin α; 3) sin2 α —0,75; 4) 4 cos2 α — 3.
1827. 1) √3 + ctg α; 2) √3 • tg α —1; 3) 3 — tg2 α; 4) 1 — 3 ctg2 α.
1828. 1) sin х + √3 • cos x; 2) √3 • sin x — cos x ;
3) a sin x + b cos x; 4) a sin ωx + b cos ωx.
1829. 1) 4 sin α — 3cos α; 2) 3sin 20° + 4 cos 20°;
3) 2 sin α — √5 cos α; 4) 12 sin 3α + 5 cos 3α.
1830. 1)1 — 2 cos2 α/2 + √3 • sin α;
2) 8 sin (45° — A) + 15 sin (45° + A);
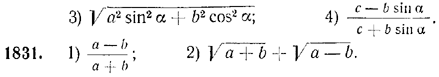
1832. Дано: sin α — sin β = m; cos α + cos β = n.
Найти sin (α — β) и cos (α — β).
Преобразовать в произведение:
1833. 1) sin α + sin β + sin (α — β); 2) 1 + cos α + cos β+ cos (α — β).
1834. 1) 1 + sin α + cos α + tg α; 2) 1 + sin α — (cos α + ctg α).
1835. 1) sin α + cos 2α + sin 3α + cos 4α; 2) cos α + sin 2α + cos 3α + sin 4α.
1836. 1) sin 3α — sin 2α • cos α; 2) cos α — sin α • sin 2α.
1837. 1) √1 + cos α + √1— cos α, 0°< α <90°;
2) √1 + cos α — √1— cos α, 0°< α <90°.
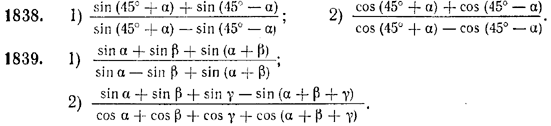
Проверить равенства.
1840. 1) sin 35° + sin 25° = cos 5°; 2) cos 12° — cos 48° = sin 18°;
3) sin 40° + cos 70° = cos 10°; 4) cos 20° — sin 50° = sin 10°;
5) tg 20° + 4 sin 20° = √3; 6) √3 • ctg 20° — 4 cos 20° = 1;
7) √3— 2 sin 10° = 4 sin 25° • cos 35°;
8) √2 +2 sin 15° = 2 cos 15°.
Доказать тождества.
1841. 1) sin2 (α + β) — sin2 (α — β) = sin 2α • sin 2β;
2) cos2 (α — β) — cos2 (α + β) = sin 2α • sin 2β.
1842. 1) √1 + sin α — √1— sin α = 2 sin α/2 , если 0°< α <90°;
2) √1 + sin α + √1— sin α = 2 cos α/2 , если 0°< α <90°.
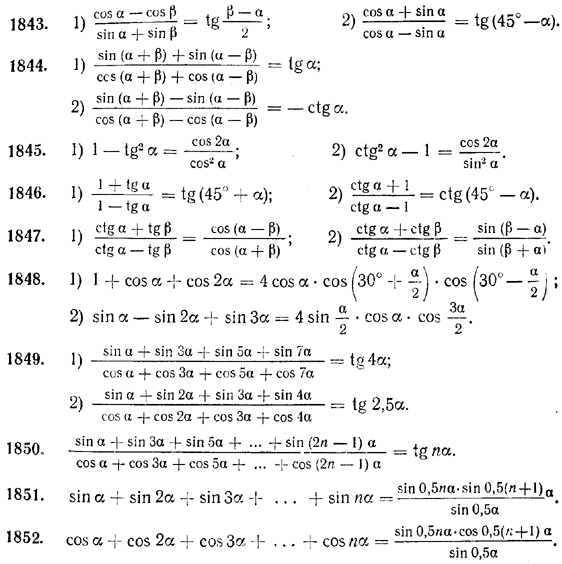
1853. Дано: sin α + sin β = 2 sin (α + β). Доказать: tg α/2 • tg β/2 = 1/3.
1854. Предполагая, что А, В, С — углы треугольника, доказать тождества:
1) sin А + sin В + sin С = 4 cos A/2 • cos B/2 • cos C/2;
2) sin A + sin В — sin С = 4 sin A/2 • sin B/2 • sin C/2;
3) tg A + tg B + tg C = tg A • tg B • tg C;
4) sin A • cos B • cos С + cos A • sin B • cos C + cos A • cos B • sin С = sin A • sin В • sin C;
5) ctg A/2 + ctg B/2 + ctg C/2 = ctg A/2 • ctg B/2 • ctg C/2;
6) cos A/2 • sin B/2 • sin C/2 + sin A/2 • cos B/2 • sin C/2+ sin A/2 • sin B/2 • cos C/2 =
= cos A/2 • cos B/2 • cos C/2;
7) sin 2A + sin 2B + sin 2C = 4 sin A • sin В • sin С;
8) sin2 A + sin2 В + sin2 С — 2 = 2 cos A • cos В • cos C;
9) sin2 A + sin2 В — sin2 С = 2 sin A • sin В • sin C;
![]()
1855. Тангенсы двух углов треугольника равны соответственно 1,5 и 5. Найти третий угол треугольника.
1856. Углы треугольника связаны соотношением
sin2 A + sin2 B — cos (A — В) • соs С — cos2 С = 0,25.
Определить угол С.
1857. Преобразовать в произведение cos2 α + cos2 β — cos2 γ, если α + β + γ = π/2
1858. Определить вид треугольника ABC, в котором углы A и В удовлетворяют соотношению
sin (A — В) = sin2 A — sin2 B.
1859. При каких значениях х на интервале [0, π] следующие функции принимают наибольшее значение:
1) у = sin x + cos x; 2) у = sin x — cos x?
Найти это наибольшее значение функции.
1860. Найти наибольшее и наименьшее значения функций:
1) 0,5 sin 2х + cos2 х ; 2) sin2 x — sin x • cos x;
3) a sin x + b cos х; 4) 5 sin2 x + 4 sin x • cos x + 2cos2 x.
1861. Доказать, что из всех треугольников с данным основанием и данным углом при вершине наибольшую площадь имеет равнобедренный треугольник.
1862. Найти наибольшее значение суммы катетов прямоугольного треугольника, имеющего данную гипотенузу с.
1863. Найти наименьшее значение площади прямоугольного треугольника, имеющего данную высоту h (опущенную на гипотенузу).
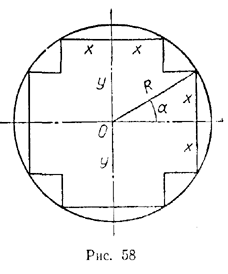
1864. При конструировании трансформаторов переменного тока стремятся к тому, чтобы железный сердечник крестообразного сечения возможно больше заполнял внутреннюю область цилиндрической катушки. Принимая радиус сечения катушки равным R, определить размеры х и у сечения сердечника (рис. 58).
1865. Решить уравнения:
1) cos x + cos 2x = 0; 2) cos x = cos 5x;
3) sin 3x + sin x = 2 sin 2x; 4) tg 5x + tg 3x = 0;
5) sin (x + π/5 ) — sin (x + 2π/15 ) = 0;
6) 1 — sin 5x = (cos 3x/2 — sin 3x/2)2 ;
7) sin4 x — cos4 x = sin 2x; 8) sin x • sin 7x = sin 3x • sin 5x;
9)√3 • sin x/2 —3 = sin x/2 + cos x/2;
10) cos x + cos у — cos (x + y) = 3/2.
1866*. Решить неравенства:
1) sin πx • (cos πx — sin πx) > 1/2 tg 2πx ;
2) sin x — √3 cos x > 1.
Лабораторная работа № 8
1) Зная, что cos 30° = √3/2 ≈ 0,8660 и применяя формулы половинного аргумента, найти синус и косинус углов 15°, 7°30', 3°45', 1°52'30" и 0°56'15".
2) Пользуясь формулами синуса и косинуса двойного аргумента и теоремами сложения для синуса и косинуса, найти значения синуса и косинуса углов, кратных 0°56'15", т. е. 0°56'15", 1°52'30", 2°48'45", 3°45'00", 4°41'15", ..., 45°00'00".
3) Используя данные, полученные при вычислении, составить таблицу значений синуса и косинуса с шагом в 0°56'15".
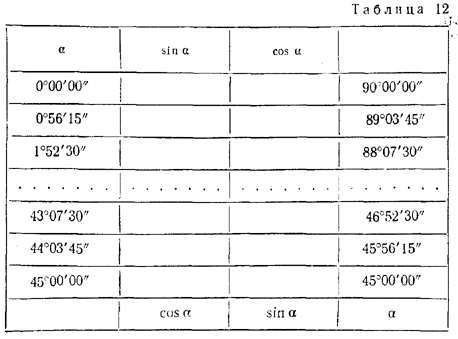
ОТВЕТЫ