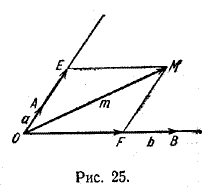
Глава I. Векторы на плоскости и в пространстве

§ 8. Разложение вектора на плоскости по двум неколлинеарным  векторам.

Пусть векторы а и b неколлинеарны. Тогда, если числа х и у удовлетворяют условию

х • а + у • b = 0,                                 (1)

то х = 0 и у = 0.

В самом деле, если, например, х =/= 0, то из (1) слeдует, что

а = —  ^y/_x • b

А это противоречит   тому,   что векторы а и b неколлинеарны. Таким образом, х = 0.

Аналогично доказывается, что и у = 0.

Говорят, что вектор а является линейной комбинацией векторов a₁, a₂, a₃, ..., a_n, если он представим в виде

а = x₁a₁+ x₂a₂+ x₃a₃+ ...+ x_na_n,

где x₁ , x₂ ,..., x_n — некоторые числа.

Так, вектор а = 3a₁ — 5a₂ + ¹/₂ a₃ есть линейная комбинация векторов a₁, a₂ и a₃.

Теорема. Любой вектор m на плоскости может быть представлен, и притом единственным образом, в виде линейной комбинации двух любых неколлинеарных векторов а и b:

.             m = х • а + у • b.        (2)

Если вектор т коллинеарен одному из векторов а и b (например, вектору а), то для некоторого числа х имеем

т =  х • а  = х • а  + 0 • b.

Тем самым вектор т представлен в виде (2).

Если же вектор т не коллинеарен ни вектору а, ни вектору b (рис. 25), то, проведя через точку М прямые, параллельные [ОВ) и [ОА), имеем

m =  OE^> +  OF^>.

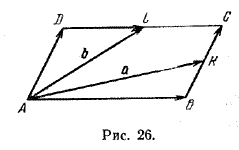
Но тогда по признаку коллинеарности векторов существуют такие числа х и у, что OE^>= ха,  OF^> = yb, откуда и вытекает равенство (2).

Докажем единственность такого представления. Пусть

т = x₁a  + у₁b   и   т = x₂a  + у₂b.

Тогда (x₁ — x₂)а + (у₁ — у₂)b = 0. Но так как векторы а и b неколлинеарны, то равенство возможно только при x₁ = x₂ и у₁ = у₂. Единственность доказана.

Если вектор представлен в виде линейной комбинации каких-то векторов, то говорят, что вектор разложен по этим векторам.

Базисом на плоскости называются два любых неколлинеарных вектора этой плоскости, взятые в определенном порядке.

Пусть e₁ и e₂ — некоторый базис и а — произвольный вектор, тогда по доказанной теореме существуют два числа х и у такие, что

а = хe₁ + уe₂.

Числа х и у называются координатами вектора а в данном базисе. В этом случае пишут а = (х; у).

Задача 1. Точки К и L—середины сторон ВС и CD параллелограмма ABCD. Разложить вектор ВС по векторам   а =  AK^> и   b = AL^>.

Из  /\  АКВ (рис. 26) имеем

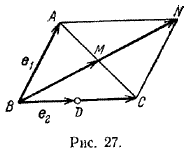
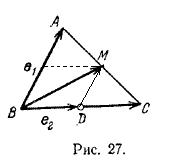
Задача 2. Дан  /\  АВС, D   [ВС], |BD| = |DC|, [ВМ] — медиана  /\ АВС.  Найти    координаты    вектора ВМ, если направленные отрезки BA^> и BD^> определяют базисные векторы.

Достроим  /\  АВС    до    параллелограмма    ABCN  (рис. 27).

Тогда BN^> = 2BM^> = BA^> + BC^>. Обозначив BA^> = e₁,  BD^> = e₂,   получим   

2BM^>= 1 • e₁ + 2 • e₂,   

откуда

  BM^> = ¹/₂ • e₁ + 1 • e₂.

Итак, в данном базисе BM^> = (¹/₂; 1).

_________________________________________________________________________

Другой вариант решения задачи авторами не рассматривается, хотя он, возможно, проще и нагляднее. Достаточно лишь провести вектор DM^> . При этом |DM| - средняя линия /\  АВС, (что вытекает из условия задачи) и, следовательно,   DM^> = ¹/₂ • BA^>