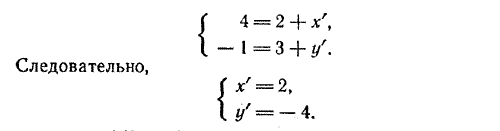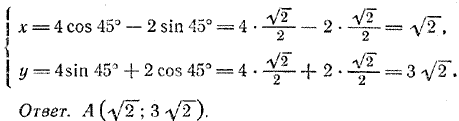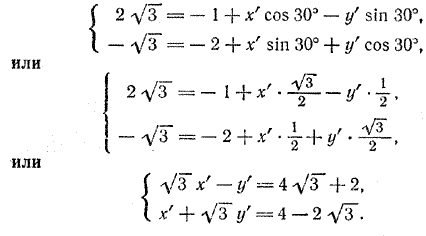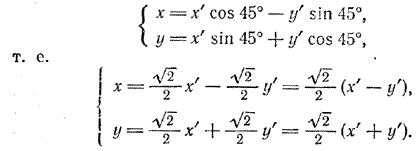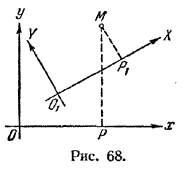
Глава I. Векторы на плоскости и в пространстве

§ 13. Переход от одной прямоугольной декартовой системы координат к другой

Данную тему мы предлагаем Вам рассмотреть  в двух вариантах.

1) По учебнику И.И.Привалов "Аналитическая геометрия" (учебник для высших технических учебных заведений 1966 г.)

2) По рассматриваемому нами учебнику Г.Н.Яковлев "Геометрия"

***

И.И.Привалов "Аналитическая геометрия"

§ 1. Задача преобразования координат.

Положение точки на плоскости определяется двумя координатами относительно некоторой системы координат. Координаты точки изменятся, если мы выберем другую систему координат.

Задача преобразования координат состоит в том, чтобы, зная координаты точки в одной системе координат, найти ее координаты в другой системе.

Эта задача будет разрешена, если мы установим формулы, связывающие координаты произвольной точки по двум системам, причем в коэффициенты этих формул войдут постоянные величины, определяющие взаимное положение систем.

Пусть даны две декартовы системы координат хОу и XO₁Y (рис. 68).

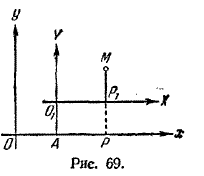
Положение новой системы XO₁Y относительно старой системы хОу будет определено, если известны координаты а и b нового начала O₁ по старой системе и угол α между осями Ох и О₁Х. Обозначим через х и у координаты произвольной точки М относительно старой системы, через X и Y—координаты той же точки относительно новой системы. Наша задача заключается в том, чтобы старые координаты х и у выразить через новые X и Y. В полученные формулы преобразования должны, очевидно, входить постоянные a, b и α.

Решение этой общей задачи мы получим из рассмотрения двух частных случаев.

1.  Меняется начало координат, направления же осей остаются неизменными (α = 0).

2.  Меняются направления осей, начало же координат остается неизменным (а = b = 0).

§ 2. Перенос начала координат.

Пусть даны две системы декартовых координат с разными началами O и O₁ и одинаковыми направлениями осей (рис. 69).

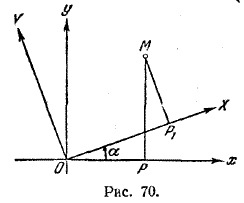
Обозначим через а и b координаты нового начала О₁ в старой системе и через х, у и X, Y—координаты произвольной точки М соответственно в старой и новой системах. Проектируя точку М на оси О₁Х и Ох, а также точку О₁ на ось Ох, получим на оси Ох три точки О, А и Р. Величины отрезков ОА, АР и ОР связаны следующим соотношением:

| ОА | + | АР | = | ОР |.         (1)

Заметив, что | ОА |  = а, | ОР | = х,  | АР | = | О₁Р₁ | = Х , перепишем равенство (1) в виде:

а  +  X  =  x   или    x = X + а.        (2)

Аналогично,    проектируя    М   и    О₁    на    ось    ординат,    получим:

y = Y + b                               (3)

Итак, старая координата равна новой плюс координата нового начала по старой системе.

Из формул  (2)  и  (3)  новые  координаты  можно  выразить через старые:

Х = х — а,                      (2')

Y = y — b.                       (3')

§ 3. Поворот осей координат.

Пусть даны две декартовы системы координат с одинаковым началом О и разными направлениями осей (рис. 70).  

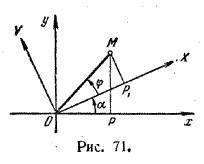
Пусть α  есть   угол  между  осями   Ох и ОХ. Обозначим через х, у и X, Y координаты произвольной точки М соответственно в старой и новой системах:

х = | ОР | ,  у = | РM | ,

X =  | ОР₁ |, Y = | Р₁M |.

Рассмотрим ломаную линию ОР₁MP и    возьмем  ее  проекцию   на  ось   Ох. Замечая,  что  проекция ломаной линии равна   проекции  замыкающего отрезка (гл. I, § 8) имеем:

ОР₁MP  = | ОР |.          (4)

С другой  стороны,   проекция  ломаной  линии  равна сумме проекций ее звеньев (гл. I, § 8); следовательно, равенство (4) запишется так:

пр ОР₁ + пр Р₁M + пp MP = | ОР |                    (4')

Так как проекция  направленного  отрезка равна его величине, умноженной  на косинус  угла  между осью  проекций и осью, на которой лежит отрезок (гл. I, § 8), то

пр ОР₁ = X cos α

пр Р₁M  = Y cos (90° + α) = — Y sin α,

пp MP = 0.

Отсюда равенство (4') нам дает:

x = X cos α — Y sin α.                                 (5)

Аналогично,   проектируя   ту   же  ломаную   на  ось   Оу,  получим выражение для у. В самом деле, имеем:

пр ОР₁ + пр Р₁M + пp MP = пp ОР   = 0.

Заметив, что

пр ОР₁  = X cos (α — 90°) = X sin α,

пр Р₁M  = Y cos α,

пp MP  = — y,

будем иметь:

X sin α +  Y cos α — y = 0,

или

y = X sin α +  Y cos α.                                (6)

Из   формул  (5)  и  (6)  мы   получим   новые   координаты  X и   Y выраженными   через   старые  х  и у,   если   разрешим   уравнения (5) и (6) относительно X и  Y.

Замечание. Формулы (5) и (6) могут быть получены иначе.

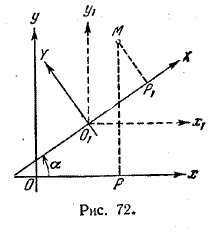
Из рис. 71 имеем:

х = ОР = ОМ cos (α + φ) =   ОМ cos α cos φ — ОМ sin α sin φ,

у = РМ = ОМ sin (α + φ) =  ОМ sin α cos φ +  ОМ cos α sin φ.

Так как (гл. I, § 11)  OM cos φ = X,    ОМ sin φ =Y,  то

x = X cos α — Y sin α,                                (5)

y = X sin α +  Y cos α.                                (6)

§ 4. Общий случай.

Пусть даны две декартовы системы координат с разными началами и разными направлениями осей (рис. 72).

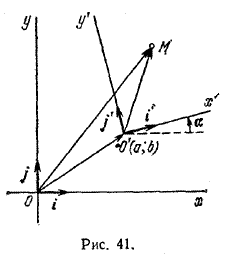
Обозначим через а и b координаты нового начала О, по старой системе, через α —угол поворота координатных осей и, наконец, через х, у и X, Y — координаты произвольной точки М соответственно по старой и новой системам.

Чтобы выразить х и у через X и Y, введем вспомогательную систему координат x₁O₁y₁, начало которой поместим в новом начале О₁, а направления осей возьмем совпадающими с направлениями старых осей. Пусть x₁ и y₁, обозначают координаты точки М относительно этой вспомогательной системы. Переходя от старой системы координат к вспомогательной, имеем (§ 2):

х = х₁+ а,   у = у₁ + b.

Переходя, далее, от вспомогательной   системы  координат   к новой,   найдем (§ 3):

х₁ = X cos α — Y sin α,      y₁ = X sin α +  Y cos α.

Заменяя х₁ и y₁ в предыдущих формулах их выражениями из последних формул, найдем окончательно:

x = X cos α — Y sin α + a                          

y = X sin α +  Y cos α + b                       (I)

Формулы (I) содержат как частный случай формулы §§ 2 и 3. Так, при α  = 0 формулы (I) обращаются в

x = X + а,      y = Y + b,

а при а = b = 0 имеем:

x = X cos α — Y sin α,      y = X sin α +  Y cos α.

Из формул (I) мы получим новые координаты X и Y выраженными через старые х и у, если уравнения (I) разрешим относительно X и Y.

Отметим весьма важное свойство формул (I): они линейны относительно X и  Y, т. е. вида:

x = AX + BY + C,   y = A₁X + B₁Y + C₁.

Легко  проверить,   что   новые  координаты   X и Y выразятся  через старые х и у тоже формулами первой  степени  относительно х и у.

***

Г.Н.Яковлев "Геометрия"

§ 13. Переход от одной прямоугольной декартовой системы координат к другой

Выбором прямоугольной декартовой системы координат устанавливается взаимно однозначное соответствие между точками плоскости и упорядоченными парами действительных чисел. Это означает, что каждой точке плоскости соответствует единственная пара чисел и каждой упорядоченной паре действительных чисел соответствует единственная точка.

Выбор той или иной системы координат ничем не ограничен и определяется в каждом конкретном случае только соображениями удобства. Часто одно и то же множество приходится рассматривать в разных координатных системах. Одна и та же точка в разных системах имеет, очевидно, различные координаты. Множество точек (в частности, окружность, парабола, прямая) в разных системах координат задается различными уравнениями.

Выясним, как преобразуются координаты точек плоскости при переходе от одной координатной системы к другой.

Пусть на плоскости заданы две прямоугольные системы координат: О, i, j и О', i', j' (рис. 41).

Первую систему с началом в точке О и базисными векторами i и j условимся называть старой, вторую — с началом в точке О' и базисными векторами i' и j'  — новой.

Положение новой системы относительно старой будем считать известным: пусть точка О' в старой системе имеет координаты (a;b), a вектор i' образует с вектором i угол α. Угол α отсчитываем в направлении, противоположном движению часовой стрелки.

Рассмотрим произвольную точку М. Обозначим ее координаты в старой системе через (х;у), в новой — через (х';у'). Наша задача — установить зависимость между старыми и новыми координатами точки М.

Соединим попарно точки О и О', О' и М, О и М. По правилу треугольника получаем

OM^> = OO'^> + O'M^>.                      (1)

Разложим векторы OM^> и OO'^> по базисным векторам i и j, а вектор O'M^> по базисным векторам i' и j' :

OM^> = xi + yj,     OO'^>= ai + bj  ,  O'M^> = x'i '+ y'j '

Теперь равенство (1) можно записать так:

xi + yj = (ai + bj) + ( x'i '+ y'j ' ).               (2)

Новые базисные векторы i' и j'  раскладываются   по старым базисным векторам i и j следующим образом:

i' = cos α i + sin α j,

j'  = cos (^π/₂ + α) i + sin ( ^π/₂ + α) j = — sin α i + cos α j.

Подставив найденные выражения для i' и j'  в формулу (2), получим векторное равенство

xi + yj  = ai + bj + х'(cos α i + sin α j) +  у' (— sin α i + cos α j)

равносильное двум числовым равенствам:

Формулы (3) дают искомые выражения для старых координат х и у точки через ее новые координаты х' и у'. Для того чтобы найти выражения для новых координат через старые, достаточно решить систему уравнении (3) относительно неизвестных х' и у'.

Итак, координаты точек при переносе начала координат в точку (а; b) и повороте осей на угол α преобразуются по формулам (3).

Если изменяется только начало координат, а направления осей остаются прежними, то, полагая в формулах (3) α = 0, получаем

Эти формулы кратко называют формулами переносa.

Если начало координат остается прежним, а оси поворачиваются на угол α, то, полагая в формулах (3) а = b = 0, получаем

Формулы  (5)  называют формулами поворота.

Задача 1. Пусть координаты нового начала в старой системе (2; 3), а координаты точки А в старой системе (4; —1). Найти координаты точки А в новой системе, если направления осей остаются прежними.

По формулам (4) имеем

Ответ. A (2; —4)

Задача 2. Пусть координаты точки Р в старой системе (—2; 1), а в новой системе, направления осей которой те же самые, координаты этой точки (5; 3). Найти координаты нового начала в старой системе.

А По формулам (4) получаем

откуда а = — 7,    b = — 2.

Ответ. (—7; —2).

Задача 3. Координаты точки А в новой системе (4; 2). Найти координаты этой точки в старой системе, если начало координат осталось прежним, а оси координат старой системы повернуты на угол α = 45°.

По формулам (5) находим

Задача 4. Координаты точки A  в старой системе (2 √3 ; — √3 ). Найти координаты этой точки в новой системе, если начало координат старой системы перенесено в точку (—1;—2), а оси повернуты на угол α = 30°.

По формулам (3) имеем

Решив эту систему уравнений   относительно х' и у', найдем: х' = 4, у' = —2.

Ответ. A (4; —2).

Задача 5. Дано уравнение прямой у = 2х — 6. Найти уравнение той же прямой в новой системе координат, которая получена из старой системы поворотом осей на угол α = 45°.

Формулы поворота в данном случае имеют вид

Заменив в уравнении прямой у = 2х — 6 старые переменные х и у новыми, получим уравнение

^√2/₂ ( x' + y' ) = 2•^√2/₂ ( x' — y' ) — 6 ,

которое после упрощений принимает вид     y'  = ^x'/₃— 2√2