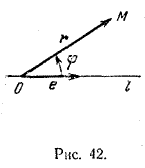
Глава I. Векторы на плоскости и в пространстве

§ 14. Полярная система координат.

Познакомимся еще с одним способом определения положения точки на плоскости при помощи чисел — полярной системой координат.

Рассмотрим на плоскости ось l с единичным вектором е и началом отсчета О (рис. 42).

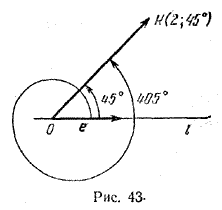
Пусть М произвольная точка плоскости, не совпадающая с точкой О. Тогда OM^> — радиус-вектор точки М относительно точки О.

Пусть r — длина вектора OM^>, т. е. | OM^> | = r, а  φ — угол между осью l и радиус-вектором   OM^>. Угол φ =    будем отсчитывать от оси l в положительном направлении, т. е. в направлении, противоположном движению часовой стрелки.

Числа r и φ называются полярными координатами точки М:  r — полярный радиус,     φ — полярный угол.

Ось l называется полярной осью, а точка О — полюсом.

Полярный радиус точки О принимается равным нулю, полярный угол точки О не определяется.

Если точка М имеет полярные координаты r и φ, то пишут М ( r ; φ). Например, точка К (рис. 43) имеет координаты  r = 2, φ = 45°, т. е. K (2; 45°).

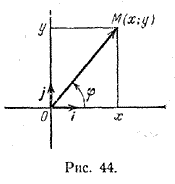
Очевидно, что положение точки на плоскости полностью определяется заданием ее полярных координат.

Если r  > 0, а φ — произвольное число, то существует (и притом только одна) точка М такая, что

| OM^> | = r   и    = φ.

Если r = 0, то точка совпадает с полюсом.

Отметим, что полярный угол точки, не совпадающей с полюсом, определяется неоднозначно. Например, полярным углом для точки K (см. рис. 43) является не только угол φ = 45°, но и угол φ  = 405° и, вообще, любой угол φ = 45° + 360°k, где  k = 0, ±1, ±2 ... .

Полярный угол точки определяется с точностью до слагаемого, кратного 360°. Если r  > 0, то пары чисел (r ; φ) и (r ; φ + 360°k), где k = 0, ±1, ±2 ..., определяют одну и ту же точку плоскости. Чтобы соответствие между точками плоскости (за исключением полюса) и их полярными координатами было взаимно однозначным на полярный угол φ накладывают ограничение 0 < φ < 360°.

Установим связь между полярными и прямоугольными декартовыми координатами одной и той же точки М плоскости.

Пусть на плоскости задана прямоугольная декартова система координат О, i, j (рис. 44).

Примем начало координат —точку О —за полюс, ось абсцисс — за полярную ось l. Тогда луч [О у) оси ординат направлен под углом 90° к оси l.

Очевидно, декартовы координаты точки М выражаются через ее полярные координаты следующим образом:

х = r cos φ,      y = r sin φ.                     (1)

Формулы (1) позволяют находить прямоугольные декартовы координаты точки по ее полярным координатам. Из формулы (1) получаем

х² + у² = r² cos² φ + r² sin² φ =  r² ( cos² φ + sin² φ) = r²,

и, следовательно,

r = √ x² + y ²   .                        (2)

Если r =/= 0   ( М не совпадает с точкой О), то из (1) и (2) следует

Формулы (2), (3) позволяют переходить от прямоугольных декартовых координат точки к ее полярным координатам.

Задача 1. Найти полярные координаты точки М (—1; √3  ).

По формуле (2) находим

По формулам (3) имеем

cos φ = ^—1/₂ = — ¹/₂ ,    sin φ = ^√3/₂,

откуда φ = 120°. Итак, М (2; 120°).

Задача 2. Найти прямоугольные декартовы координаты точки М(4; 135°).

По формулам (1) имеем

х = 4 • cos135° = 4 • (— ^√2/₂) = — 2√2  ,

у = 4 • sin 135° = 4 • ^√2/₂ = 2√2 .

Итак, М (— 2√2 ; 2√2  ).