Глава I. Векторы на плоскости и в пространстве

§ 23*. Смешанное произведение трех векторов и его свойства

Смешанным произведением трех векторов а, b, с называется число, равное скалярному произведению вектора [а; b] на вектор с.

Смешанное произведение векторов a, b и с обозначается (а; b; с). Следовательно,

(а; b;с) = | [а; b] | • |с | • cos ψ,                   (1)

где ψ — угол между векторами [а; b] и с.

Теорема 1. Модуль смешанного произведения трех некомпланарных векторов а, b и с равен объему параллелепипеда, построенного на векторах-множителях.

Как известно (§ 21), площадь S параллелограмма, построенного на векторах а и b, равна | [а; b] |. Поэтому из формулы (1) следует, что

(а; b;с) = S • |с | • cos ψ.

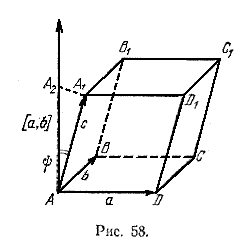
С другой стороны, объем V параллелепипеда, построенного на векторах а, b, с (рис. 58), равен произведению площади его основания S на высоту h, причем h = |AA₂|, где А₂ — проекция вершины А₁ на ось, определяемую вектором [а; b].

Так как |AA₂| = |с | • cos ψ, то

V = S • h = S • | c | • | cos ψ | = | (а; b;с)  |.

Из формулы (1) видно, что если смешанное произведение трех векторов не равно кулю, то его знак совпадает со знаком cos ψ. Поэтому смешанное произведение положительно, если вектор с напразлен в ту же сторону от плоскости векторов а и b, что и вектор  [а; b], т. е. если тройка векторов а, b, с правая.

Смешанное произведение отрицательно, когда вектор с и вектор [а; b] направлены в противоположные стороны от плоскости век-, торов а и b, т. е. когда тройка векторов а, b, с левая.

Итак, если векторы а, b, с образуют правую тройку, то (а; b;с)  > 0, если левую, то (а; b;с) < 0.

Теорема 2. Смешанное произведение трех векторов равно нулю тогда и только тогда, когда векторы компланарны.

Необходимость. Пусть (а; b, с) = 0. Предположим, что векторы а, b и с некомпланарны. Построим на этих векторах параллелепипед.

Его объем V > 0, но по теореме 1  | (а; b;с)  | = V, что противоречит предположению.

Достаточность. Пусть векторы а, b и с компланарны. Тогда вектор [а; b] перпендикулярен вектору с, но скалярное произведение перпендикулярных векторов равно нулю, т. е.  [а; b]  • c  = (а; b;с) = 0.

Рассмотрим некоторые свойства смешанного произведения.

1. Для любых векторов а, b и с справедливы равенства

(а; b;с) = (b; с, а) = (с; а; b),

т. е. при циклической перестановке множителей смешанное произведение не изменяется.

Достаточно доказать первое равенство, так как второе следует из первого.

Если векторы а, b и с компланарны, то равенство (а; b;с) = (b; с, а) очевидно; обе части равенства равны нулю.

Пусть векторы а, b и с некомпланарны. Тогда в силу теоремы 1

| (a;b;c) | = V   и   | (b;c;a) | = V,

где V — объем параллелепипеда, построенного на данных трех векторах. Но тройки векторов а, b, с и b, с, а являются одновременно либо правыми, либо левыми, поэтому знаки чисел (a;b;c) и (b;c;a) совпадают.

2. Для любых векторов а, b и с справедливы равенства

(a;b;c) = — (b; а;с) = — (а; с; b),

т. е. при перестановке двух соседних множителей знак смешанного произведения изменяется на противоположный.

Первое из равенств следует из свойства векторного произведения (§ 21):

(a;b;c) = [а; b]  • с = — [b; а]  • с  = — (b; а;с).

Второе равенство очевидно в силу свойства  1  смешанного произведения.

Задача   1. Вычислить (a;b;c) , если векторы а, b, с образуют правую тройку, a _|_ c,     b _|_ c , (a;^{^}b) =150°,| а | = | b | = 4 , | c | = 3

По определению

(a;b;c) = [а; b]  • с = | а | • | b | • sin 150° • | c | • cos 0° = 4 • 4 • 3 • ¹/₂ = 24.

Задача   2. Вычислить ( i + j;  j — 2i;  k ), где i, j, k — взаимно    перпендикулярные   единичные векторы, образующие правую тройку.

( i + j;  j — 2i;  k ) = [i + j;  j — 2i] • k =  ([i; j] — 2[i; i] + [j; j] —  2[j; i]) • k =

= 3[i; j] • k = 3 (i; j; k) = 3.