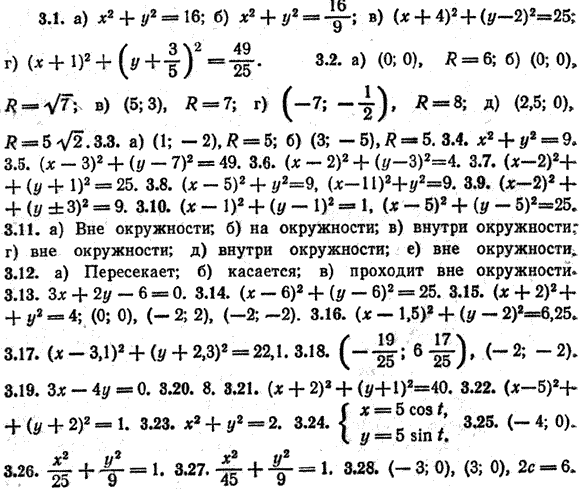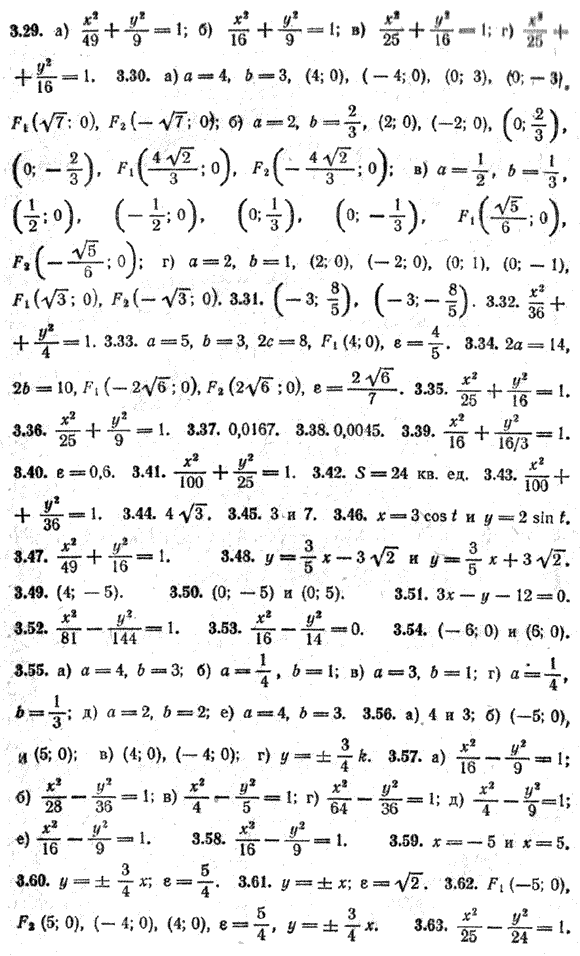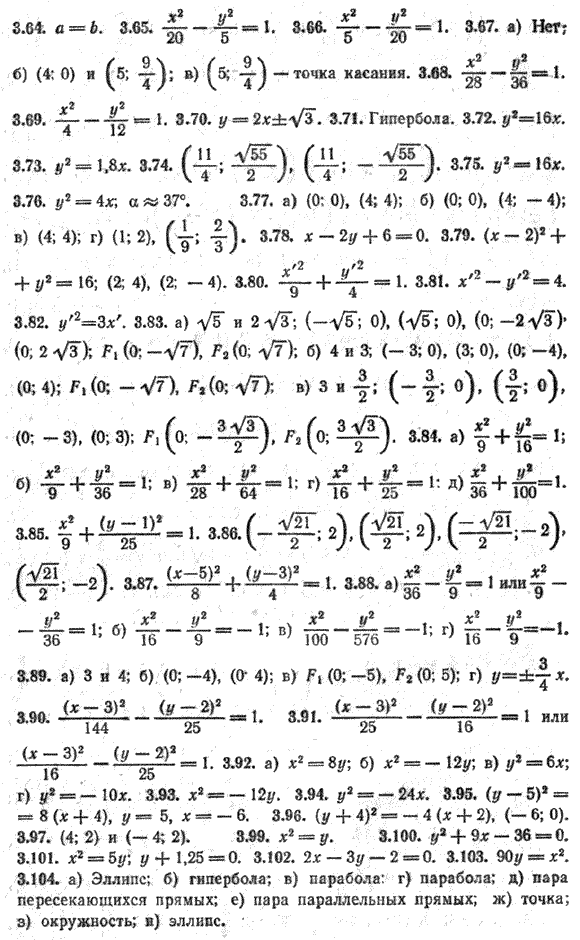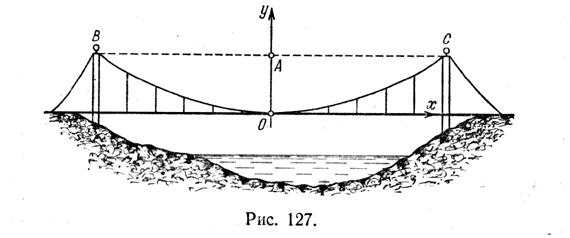
Глава III. Кривые второго порядка

Задачи к главе III

3.1. Составьте уравнение окружности:

а) радиуса R = 4 с центром в начале координат;

б) радиуса R = ⁴/₃ с центром в начале координат;

в) радиуса R = 5 с центром в точке С(—4; 2);

г) радиуса R = ⁷/₅    с центром в точке D (— 1; — ³/₅)

3.2. Найдите центр и радиус окружности:

а) х² + у² = 36;

б) х² + у² = 7;

в) (х—5)² + ( у —3)² = 49;

г) (х + 7)² + (у + ¹/₂)² = 64;

д) (х — 2,5)² + у² = 50.

3.3. Докажите, что данное уравнение является уравнением окружности. Найдите ее центр и радиус:

а) х²  — 2х + 4у + у² — 20 = 0;

б) х²  — 6х + 10у + у² + 9 = 0.

3.4. Составьте уравнение окружности, центр которой совпадает с началом координат, если окружность касается прямой х = 3.

3.5. Напишите уравнение окружности, центр которой находится в точке С(3; 7), если известно, что она касается оси Ох.

3.6. Напишите уравнение окружности, центр которой находится  в точке пересечения прямых 2х + 3у—13 = 0, х + у— 5 = 0, если она касается оси ординат.

3.7. Напишите уравнение окружности, проходящей через точку N(6 ; 2) с центром в точке С(2; — 1).

3.8. Напишите уравнение окружности, центр которой лежит на оси абсцисс, если окружность касается прямых х =8 и у = 3.

3.9. Напишите уравнение окружности, если известно, что она касается оси абсцисс и прямых х = — 1 и х = 5.

3.10. Напишите уравнение окружности, проходящей через точку М (2; 1) и касающейся осей координат.

3.11. Определите, как расположена точка М(—2; 1) относительно каждой из окружностей (внутри, вне или на окружности):

а) х² + у²  = 2;        б) х² + у²  — 5 = 0;

в) х² + у²  = 25;      г) х² + у²  — 8х — 4у = 5;

д) х² + у²  + 6х — 8у = 0;        е) х² + у² = 0,01.

3.12. Определите, как расположена прямая относительно окружности (пересекает, касается или проходит вне ее), если прямая и окружность заданы следующими уравнениями;

а) 2х — у — 3 = 0    и    х² + у² — 3х + 2у — 3 = 0;

б) х — 2у — 1= 0    и   (х — 4)²  + (у + 1)²  = 5;

в) х + 3у + 10 = 0  и    х² + у² = 1

3.13. Найдите уравнение линии центров двух окружностей
(х — 2)²  + у²  = 16   и   х²  + (у — 3)²  = 9.

3.14. Даны точки M₁(2; 3) и М₂(10; 9). Напишите уравнение окружности, диаметром которой служит отрезок М₁М₂.

3.15. Окружность касается оси ординат в начале координат и проходит через точку
М₁(— 4; 0). Напишите уравнение окружности и найдите точки пересечения ее с биссектрисами координатных углов.

3.16. Напишите уравнение окружности, проходящей через три точки
М₁(0; 0), М₂(3; 0) и М₃(0; 4).

3.17. Напишите уравнение окружности, описанной около треугольника, стороны которого принадлежат прямым
 х — 3у + 1 = 0,   9х — 2у — 41 = 0,    7х + 4у + 7 = 0.

3.18. Определите координаты точек пересечения прямой у — 7х — 12 = 0 и окружности (х — 1)²+ (у — 2)² = 25.

3.19. Напишите уравнение диаметра окружности х² + у² = 25, перпендикулярного прямой   4х  + 3у — 25 = 0.

3.20. Вычислите кратчайшее расстояние от точки A (8; —6) до окружности  
х² + у²  — 4 = 0.

3.21. Напишите уравнение окружности, проходящей через точки M(4; 1) и N(0; 5), если известно, что центр ее находится на прямой х + у + 3 = 0.

3.22. Найдите уравнение окружности, симметричной окружности
(х— 1)²+ (у — 2)² = 1 относительно прямой у = х — 3.

3.23. Окружность задана уравнениями:  x = √2  cos t,  y = √2 sin t    0 < t  < 2π.   Запишите каноническое уравнение этой  окружности.

3.24. Окружность задана уравнением х² + у² = 25. Запишите параметрические уравнения этой окружности.

3.25. Окружности заданы  уравнениями  x = 4 cos t,  y = 4 sin t    0 < t  < 2π   и
(х— 1)² + у² = 25. Найдите точки пересечения данных окружностей.

3.26. Напишите каноническое уравнение эллипса, если фокальное расстояние равно 8 и эллипс проходит через точку (0; —3).

3.27. Напишите каноническое уравнение эллипса, если его фокус находится в точке
(6; 0) и ось ординат эллипс пересекает в точке (0; —3).

3.28. Докажите, что уравнение 7x² + 16у² — 112 = 0 является уравнением эллипса. Найдите координаты фокусов и фокальное расстояние.

3.29. Напишите каноническое уравнение эллипса, если:

а) его полуоси равны 7 и 3;

б) его полуоси равны 3 и 4;

в) его большая полуось равна 5, а фокусное расстояние равно 6;

г) его малая полуось равна 4, а фокусное расстояние равно 6.

3.30. Для каждого из следующих эллипсов определите его полуоси, координаты вершин и фокусов:

а) 9x² + 16у² = 144;    б) x² + 9у² = 4;

в) 4x² + 9у² =1;       г) 0,25x² + у² = 1.

3.31. Дан эллипс 4x² + 25у² — 100 = 0. Определите ординаты точек эллипса, абсциссы которых равны — 3.

3.32. Ординаты точек окружности х² + у² = 36 уменьшены в 3 раза по абсолютной величине. Напишите уравнение полученной новой кривой.

3.33. Дан эллипс  Найдите его большую полуось, его малую полуось, фокальное расстояние, координаты фокусов и вершин, эксцентриситет.

3.34. Дан эллипс 25x² + 49y² = 1225. Определите длины осей, координаты фокусов и эксцентриситет.

3.35. Напишите каноническое уравнение эллипса, если его. большая полуось а = 5, а эксцентриситет ε  = ³/₅.

3.36. Напишите каноническое уравнение эллипса, у которого расстояния от фокуса до концов большой оси равны 1 и 9.

3.37. Земля движется по эллиптической орбите, в одном из фокусов которой находится Солнце. Вычислите эксцентриситет земной орбиты, если ближайшая к Солнцу точка земной орбиты (перигелий) находится на расстоянии 147 млн. км от Солнца, а наиболее удаленная от Солнца точка орбиты (афелий) находится на расстоянии 152 млн. км от него.

3.38. 9 июля 1980 года в Советском Союзе произведен запуск одной ракетой-носителем восьми искусственных спутников Земли   "Космос-1192-1199". Вычислите эксцентриситет орбиты этих искусственных спутников, если все восемь спутников движутся по эллиптической орбите, в одном из фокусов которой находится центр Земли. Максимальное расстояние от поверхности Земли — 1522 км; минимальное расстояние от поверхности Земли — 1451 км. Средний радиус Земли приближенно равен 6371 км.

3.39. Напишите каноническое уравнение эллипса, если эллипс проходит через точку
М(2; —2), а его большая полуось равна 4.

3.40. Найдите эксцентриситет эллипса

3.41. Найдите каноническое уравнение эллипса, касающегося в концах своей большой оси окружности х² + у² = 100, если известно, что а = 2b.

3.42. Вычислите площадь четырехугольника, две вершины которого находятся в фокусах эллипса 9х² + 25y² — 225 = 0, а две другие вершины совпадают с концами его малой оси.

3.43. Сторона ромба равна 10. Через две противоположные его вершины проходит эллипс, фокусы которого совпадают с двумя другими вершинами ромба. Напишите уравнение эллипса, приняв диагонали ромба за оси координат, если координаты фокуса (8; 0)

3.44. Определите длину хорды эллипса  , делящей угол между осями пополам.

3.45. Дан эллипс 15х² + 25y² — 375 = 0. Через фокус проведен перпендикуляр к его большой оси. Определите расстояния от точек пересечения этого перпендикуляра с эллипсом до фокусов.

3.46. Составьте параметрические уравнения эллипса 4х² + 9y² — 36 = 0.

3.47. Даны параметрические уравнения эллипса

х = 7 cos t,     у = 4 sin t.

Запишите его каноническое уравнение.

3 48, Найдите уравнения касательных к эллипсу 9х² + 25y² =  225, угловой коэффициент которых равен  ³/₅

3.49. Найдите точку касания прямой 5х — 2у — 30 = 0 с эллипсом
75х² + 24y² — 1800 = 0.

3.50. Дан эллипс 25х² + 36y² — 900 = 0 и окружность х² + y² = 25. Найдите точки их пересечения.

3.51. Напишите уравнение касательной к эллипсу в точке (3; —3), если его уравнение 36х² + 12y² — 432 = 0.

3.52. Напишите каноническое уравнение гиперболы, если фокальное расстояние равно 30 и гипербола проходит через точку (—9; 0).

3.53. Напишите каноническое уравнение гиперболы, если ее фокус находится в точке
(— 5√2 ; 0) и ось абсцисс гипербола пересекает в точке (6; 0).

3.54. Докажите, что уравнение 11х² — 25 y² — 275 = 0 является уравнением гиперболы. Найдите координаты фокусов.

3.55. Определите полуоси каждой из следующих гипербол!

a)      б) 16х² — y² = 1;

в) х² — 9y² = 9;    г) 16х²  — 9y² = 1;

д) х² — y² = 4;      е) 9х² — 16y² = 144.

3.56. Для гиперболы 9х² — 16y² — 144 = 0 найдите:

а) полуоси;

б) координаты фокусов;

в) координаты вершин;

г) уравнения асимптот.

3.57. Напишите каноническое уравнение гиперболы, если:

а) ее действительная полуось равна 4, а мнимая — 13;

б) фокальное расстояние равно 16, а мнимая полуось — 6;

в) фокальное расстояние равно 6, а ε = 1,5;

г) действительная полуось равна 8, a ε = ⁵/₄;

д) уравнение асимптоты у = ³/₂ х, а действительная полуось равна 2;

е) мнимая полуось равна 3, а   ε = ⁵/₄ .

3.58. Напишите каноническое уравнение гиперболы, если расстояния от одной из ее вершин до фокусов равны 9 и 1.

3.59. Дана гипербола напишите уравнения параллельных прямых, ограничивающих часть плоскости, не содержащей ни одной точки гиперболы.

3.60. Найдите асимптоты гиперболы  Постройте гиперболу и найдите ее эксцентриситет.

3.61. Найдите асимптоты гиперболы х² — y² = 9. Постройте гиперболу и вычислите ее эксцентриситет.

3.62. Дано уравнение гиперболы 9х² —16 y² = 144. Найдите координаты ее фокусов и вершин, эксцентриситет и уравнение асимптот. Сделайте чертеж.

3.63. Составьте каноническое уравнение гиперболы, действительная полуось которой равна 5, а эксцентриситет 1,4.

3.64. Определите, при каком условии асимптоты гиперболы  будут взаимно перпендикулярны.

3.65. Составьте каноническое уравнение гиперболы, если уравнение ее асимптоты
у = ¹/₂ х, а один из фокусов находится в точке (—5; 0).

3.66. Напишите каноническое уравнение гиперболы, зная, что  асимптоты ее имеют уравнения у = ± 2х, а фокусное расстояние равно 10.

3.67. Дана гипербола  Найдите точки пересечения гиперболы с прямыми:

а) х — у +1=0;

б) 9х — 4у — 36 = 0;

в) 5х — 4у — 16 = 0.

3.68. Составьте уравнение гиперболы, фокусы которой находятся в вершинах эллипса  а вершины —в фокусах эллипса.

3.69. Фокусы гиперболы совпадают с фокусами эллипса 9х² + 25у² — 225 = 0. Составьте уравнение гиперболы, если ее эксцентриситет равен 2.

3.70. Найдите уравнения касательных к гиперболе х² — у² = 1, угловой коэффициент которых равен 2.

3.71. Эксцентриситет траектории движения первой советской космической ракеты, запущенной в сторону Луны 2 января 1959 г. равен 1,05. Определите вид траектории ракеты.

3.72. Напишите уравнение параболы, если координаты фокуса (4; 0), а уравнение директрисы х + 4 = 0.

3.73. Напишите каноническое уравнение параболы, проходящей через точку (5; 3).

3.74. Дана парабола у² = 5х. Найдите точки параболы, расстояние от которых до фокуса равно 4.

3.75. Составьте каноническое уравнение параболы, у которой фокус находится в точке пересечения прямой 2х — 5у — 8 = 0 с осью абсцисс. Постройте эту параболу.

3.76. Составьте каноническое уравнение параболы, проходящей через точку N(9; 6), определите угол , где F — фокус параболы.

3.77. Найдите точки пересечения параболы у² = 4х и прямых:
а) х = у;      б) х = — у;

в) х — 2у + 4 = 0;

г) 3х — 2у + 1 = 0.

Постройте чертеж.

3.78. Напишите уравнение касательной к параболе у² = 6х в точке (6; 6).

3.79. Напишите уравнение окружности, центр которой совпадает с фокусом параболы
у² = 8х, если известно, что окружность касается директрисы параболы. Определите координаты точек пересечения параболы и окружности и постройте чертеж.

3.80. Приведите уравнение эллипса   к каноническому виду.

3.81. Дана гипербола ху = 2. Приведите ее уравнение к каноническому виду.

3.82. Приведите уравнение параболы 3у = х²  + 4х — 11  к каноническому виду.

3.83. Для каждого из следующих эллипсов определите его полуоси, координаты вершин и координаты фокусов:

а) 12х² + 5у² — 60 = 0;

б) 16х² + 9у²— 144 = 0;

в) 4х² + у² = 9.

3.84. Напишите уравнение эллипса, симметрично расположенного относительно осей координат с фокусами на оси Оу, если:

а) его полуоси равны 3 и 4;

б) его полуоси равны 6 и 3;

в) его большая полуось равна 8, а фокусное расстояние равно 6;

г) его малая полуось равна 4, а эксцентриситет ε = ³/₅;

д) его малая полуось равна 6, а фокусное расстояние равно 8.

3.85. Напишите уравнение эллипса, у которого сумма полуосей равна 8 и расстояние между фокусами равно 8. Фокусы лежат на оси ординат и расположены симметрично относительно точки (0; 1).

3.86. Дан эллипс 16х²  + 7у²  — 112 = 0. Определите координаты точек эллипса, расстояние которых до фокуса равно 2,5.

3.87. Окружность (x — 5)²+ (у — 3)² = 4 касается эллипса и проходит через его фокусы. Составьте уравнение эллипса, если его большая ось параллельна оси абсцисс.

3.88. Составьте уравнение гиперболы, расположенной симметрично относительно осей координат, с фокусами на оси ординат, если

а) полуоси равны 3 и 6;

б) с = 5,  ε = ⁵/₃ ;

в) уравнение асимптоты  у =  ¹²/₅  х, а действительная полуось равна 24;

г) ε = ⁵/₃  , а мнимая полуось равна 4.

3.89. Для гиперболы 9х² — 16у²  = — 144 найдите: а) полуоси; б) координаты вершин; в) координаты фокусов; г) уравнения асимптот.

3.90. Напишите уравнение гиперболы, у которой расстояние между вершинами равно 24, а фокусы имеют координаты (— 10; 2) и (16; 2).

3.91. Составьте уравнение гиперболы, если ее полуоси равны 5 и 4, центр имеет координаты (3; 2), а действительная ось параллельна оси абсцисс.

3.92. Напишите уравнение параболы с вершиной в начале координат, если:

а) парабола расположена в верхней полуплоскости симметрично относительно оси ординат и фокальный параметр равен 4;

б) парабола расположена в нижней полуплоскости симметрично относительно оси ординат и фокальный параметр равен 6;

в) парабола расположена в правой полуплоскости симметрично относительно оси абсцисс, а ее фокальный параметр равен 3;

г) парабола расположена в левой полуплоскости симметрично относительно оси абсцисс, а ее фокальный параметр равен 5.

3.93. Напишите уравнение параболы, проходящей через начало координат и симметричной относительно оси ординат, если координаты фокуса F(0; —3).

3.94. Фокус параболы имеет координаты F(— 6; 0), а уравнение директрисы х — 6 = 0. Составьте уравнение параболы.

3.95. Найдите уравнение параболы, зная, что ее вершина находится в точке А(—4; 5), а фокус в точке В(—2; 5). Напишите уравнение ее оси и директрисы.

3.96. Дан фокус параболы (— 3; — 4) и уравнение ее директрисы х + 1 = 0. Напишите уравнение параболы и найдите точки пересечения параболы с осями координат.

3.97. Определите координаты точки, которая лежит на параболе х²  = 8у, если расстояние до этой точки от директрисы равно 4.

3.98. Постройте на одном чертеже следующие параболы:   
          х²  = ¹/₂ у   х²  = у ,  х²  = 2у.

3.99. Фокус параболы лежит в точке F (0; ¹/₄) ,  директриса параллельна оси абсцисс и отсекает на оси ординат отрезок, длина которого равна ¹/₄ . Напишите уравнение параболы.

3.100. Парабола проходит через точки A(0; 6) и В (4; 0) симметрично относительно оси абсцисс. Напишите уравнение параболы и постройте ее.

3.101. Составьте уравнение параболы и напишите уравнение ее директрисы, если парабола проходит через точки пересечения прямой у = х и окружности х² + y² — 10у = 0 и симметрична относительно оси ординат. Постройте окружность, прямую и параболу.

3.102. Напишите уравнение касательной к параболе х² = 6у в точке (2; ²/₃).

3.103. Канат подвесного моста имеет форму параболы (рис.127). Требуется составить ее уравнение относительно указанных на рисунке осей координат, если прогиб каната
 | OA | = 10, а длина моста | ВС | = 60.

3.104. Какое множество на плоскости задано следующими уравнениями второго порядка:

a) 3х² + 4y² = 12;      б) 3х² — 4y² = 12;

в) х² — 4у = 3;          г) y² — 4х = 0;

д) 25х² — 9y² = 0;     е) 5y² — 125 = 0;

ж) 36х² + 49y² = 0;    з) х² + (у — 2)² = 7;

и) 5х² — 10x + 3y² + 6y + 7 = 0.

ОТВЕТЫ