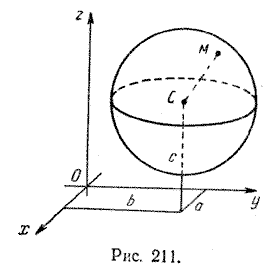
Глава VI. Простейшие криволинейные поверхности и тела вращения.

§ 73. Сфера и шар.

Множество всех точек пространства, находящихся на данном расстоянии R от данной точки С, называется сферой радиуса R с центром в точке С (рис. 211).

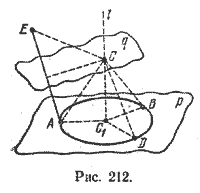
Другими словами, сфера радиуса R с центром в точке С — это множество всех точек М пространства, удовлетворяющих условию

|CM| = R.     (1)

Отрезок,    соединяющий две точки сферы и проходящий через ее центр,   называется    диаметром  сферы. Очевидно, что длина диаметра сферы   радиуса R равна 2R.

Если в пространстве задана некоторая прямоугольная декартова система кородинат и
(а; b; с) — координаты точки С, а (х; у; z) — координаты точки М, то условие (1) принимает вид

√(x — a)² + (y — b)² + (z — c)²   = R.

Отсюда следует, что сфера радиуса R с центром в точке С (а; b; с) имеет уравнение

(x — a)² + (y — b)² + (z — c)²   = R²               (2)

B частности, сфера радиуса R с центром в начале координат имеет уравнение

х² + у² + z²  = R²           (3)  

Задача 1. Составить уравнение сферы радиуса R = 5 с центром в начале координат.

Непосредственной подстановкой значения радиуса в уравнение (3) получим

х² + у² + z²  = 25.

Задача 2. Написать уравнение сферы с центром в точке С (2; —3; 5) и радиусом, равным 6.

Подставив значение координат точки С и значение радиуса в уравнение (2), получим

(x —  2)² + (y + 3)² + (z — 5)² = 36.

Задача 3. Найти центр и радиус сферы

(х + 4)² + (y — 3)² + z² =100.

Сравнивая данное уравнение с уравнением сферы (2), видим, что
  а = — 4, b = 3, с = 0, R = 10.  Следовательно, С(—4; 3; 0), R = 10.

Задача 4. Доказать, что уравнение

х² + у² + z²  — 2х + 4у — 6z + 5 = 0

является уравнением сферы.

Преобразуем левую часть данного уравнения, выделив квадраты двучленов, содержащих соответственно х, у и z:

х² — 2х + у² + 4у + z² — 6z + 5 =

= (x —  1)² —  1 + (y + 2)² — 4 + (z — 3)² — 9 + 5 =

= (x —  1)² + (y + 2)² + (z — 3)²—9.

Следовательно, данная поверхность имеет уравнение

(x —  1)² + (y + 2)² + (z — 3)² = 9.

Это уравнение представляет собой уравнение сферы с центром в точке С(1; —2; 3) и радиусом R = 3.

Множество всех точек пространства, расстояние которых от данной точки С не превосходит данного числа R, называется шаром радиуса R с центром в точке С.

Иначе, шар радиуса R с центром в точке С — это множество всех точек М пространства, удовлетворяющих условию

|CM| < R.

В координатах это условие имеет вид

(x — a)² + (y — b)² + (z — c)²   <   R².

Сфера радиуса R с центром в точке С называется поверхностью соответствующего шара. Про нее говорят, что она ограничивает шар радиуса R с центром в точке С.

Теорема. Через любые четыре точки, не лежащие в одной плоскости, проходит и притом единственная сфера.

Пусть А, В, D, Е четыре точки, не лежащие в одной плоскости. Достаточно доказать, что существует и притом единственная точка, С, равноудаленная от четырех данных точек. Очевидно, точка С и будет центром сферы, проходящей через данные точки.

Через точки А, В, D, которые, очевидно, не лежат на одной прямой, проходит   единственная   плоскость р и единственная окружность. Пусть С₁ — центр этой окружности. Очевидно, множество всех точек пространства, равноудаленных от трех точек А, В, D — это перпендикуляр l к плоскости р, проходящий через точку C₁ (рис. 212).

Рассмотрим теперь точки А и Е. Множество всех точек пространства, равноудаленных от точек А и Е, — это плоскость q, перпендикулярная прямой АЕ и проходящая через середину отрезка АЕ. Плоскость q обязательно пересечет прямую l , так как точка Е не лежит в плоскости р. Очевидно, что точка С, являющаяся пересечением плоскости q с прямой  l, будет равноудаленной от всех четырех данных точек А, В, D, Е. Из построения видно, что точка С — единственная точка пространства, удовлетворяющая этому условию.