Глава VII. Объемы тел и площади поверхностей.

§ 90. Площадь поверхности цилиндра, конуса и усеченного конуса

За площадь боковой поверхности цилиндра принимается площадь развертки его боковой поверхности.

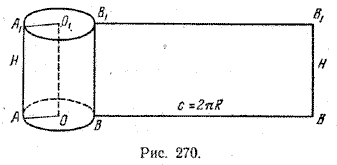
Поэтому площадь боковой поверхности прямого кругового цилиндра равна площади соответствующего прямоугольника (рис. 270) и вычисляется по формуле

S _б.ц. = 2πRH,    (1)

где R — радиус основания, а H — высота цилиндра.

Если к площади боковой поверхности цилиндра   прибавить площади двух его оснований, то получим площадь полной поверхности цилиндра

S_полн. =2πRH + 2πR²  = 2πR (H + R).

За площадь боковой поверхности конуса принимается площадь развертки его боковой  поверхности.

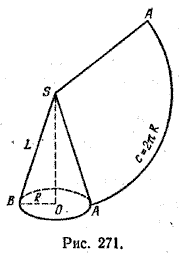
Поэтому площадь боковой поверхности прямого кругового конуса равна площади соответствующего кругового сектора (рис. 271) и вычисляется по формуле

S _б.к. = πRL,      (2)

где R — радиус основания, a L — длина образующей конуса. Если к площади боковой поверхности конуса прибавить площадь его основания, то получим площадь полной поверхности конуса

S_полн.  = πRL + πR² = πR (L + R).

Аналогично за площадь боковой поверхности усеченного конуса принимается площадь соответствующей развертки.

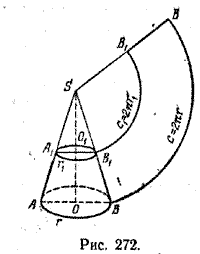
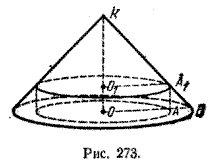
Поэтому в случае прямого кругового конуса (рис. 272) площадь боковой поверхности усеченного конуса вычисляется по формуле

S _б.у.к. = π ( r₁ + r )L

где r₁ и  r — радиусы оснований, a L — длина образующей усеченного конуса.

Задача. В конус вписан цилиндр (рис.273). Высота конуса в 4 раза больше высоты цилиндра, а длина образующей конуса в 6 раз больше высоты цилиндра. Найти отношение площадей боковых поверхностей конуса и цилиндра.

По формулам (1) и (2) получаем

S _б.ц. = 2π|OA||OO₁|,       S _б.к. = π|ОВ||KB|.

По условию |KB| = 6|OO₁|. Следовательно,

Из подобных треугольников ОВК и O₁А₁К находим

По условию |ОK | = 4|OO₁|. Следовательно,

Учитывая, что |O₁А₁| = |OA|, получаем

= 3 • ⁴/₃ = 4

т. е. площадь боковой поверхности конуса в 4 раза больше площади боковой поверхности цилиндра.