МЕТРИЧЕСКИЕ  СООТНОШЕНИЯ    МЕЖДУ  ЭЛЕМЕНТАМИ
ПРЯМОУГОЛЬНОГО  ТРЕУГОЛЬНИКА.

2.(188.) Теорема. В прямоугольном треугольнике перпендикуляр, опущенный из вершины прямого угла на гипотенузу, есть средняя пропорциональная величина между отрезками, на которые основание перпендикуляра делит гипотенузу, а каждый катет есть средняя пропорциональная между гипотенузой и прилежащим к этому катету отрезком гипотенузы.

Пусть AD (черт. 2) есть перпендикуляр, опущенный из вершины прямого угла А на гипотенузу ВС. Требуется доказать следующие три пропорции:

1)  ^BD/_AD = ^AD/_DC ;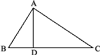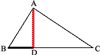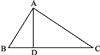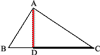      

2) ^BC/_AB =  ^AB/_BD ;      

3) ^BC/_AC = ^AC/_DC.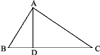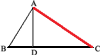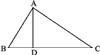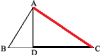      

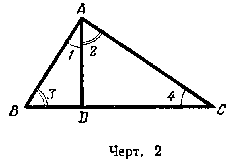
Первую пропорцию мы докажем из подобия треугольников ABD и ADC. Эти треугольники подобны, потому что

/   1 = /   4 и    /  2 = /  3

как острые углы с соответственно перпендикулярными сторонами. Возьмём в /\  ABD те стороны BD и AD, которые составляют первое отношение доказываемой пропорции; сходственными сторонами в /\  ADC  будут AD и DC¹, поэтому

BD : AD = AD : DC.

_________________________________
 ¹Чтобы безошибочно определить, какие стороны взятых треугольников сходственны между собой, полезно держаться такого пути:
 1)  указать углы, против которых лежат взятые стороны одного треугольника;
 2)  найти равные им углы в другом треугольнике;
 3)   взять противолежащие им стороны.
   Например, для треугольников ABD и ADC рассуждаем так: в. треугольнике ABD стороны BD и AD лежат против углов 1 и 3; в треугольнике ADC этим углам равны 4 и 2; против них лежат стороны AD и DC. Значит, стороны AD и DC сходственны со сторонами BD и AD.

Вторую пропорцию докажем из подобия треугольников ABC и ABD. Эти треугольники подобны, потому что они прямоугольные и острый угол В у них общий. В /\  ABC возьмём те стороны ВС и АВ, которые составляют первое отношение доказываемой пропорции; сходственными сторонами в /\  ABD будут АВ и BD; поэтому

ВС : АВ = АВ : BD.

Третью пропорцию докажем из подобия треугольников ABC и ADC. Эти треугольники подобны, потому что они оба прямоугольные и имеют общий острый угол С.
В /\  АВС возьмём стороны ВС и АС; сходственными сторонами в /\  ADC будут АС и DC; поэтому

ВС : АС = AC: DC.

3. (189.) Следствие. Пусть А (черт. 3) есть произвольная точка окружности, описанной на диаметре ВС.

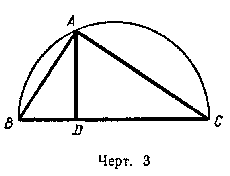
Соединив концы диаметра с этой точкой, мы получим прямоугольный /\  ABC, у которого гипотенуза есть диаметр, а катеты суть хорды (по свойству вписанного угла, опирающегося на диаметр). Применяя доказанную выше теорему к этому треугольнику, приходим к следующему заключению:

Перпендикуляр, опущенный из какой-либо точки окружности на диаметр, есть средняя пропорциональная величина между отрезками, на которые основание перпендикуляра делит диаметр, а хорда, соединяющая эту точку с концом диаметра, есть средняя пропорциональная между диаметром и прилежащим к хорде отрезком диаметра.

4. (190.) Задача. Построить отрезок, средний пропорциональный между двумя отрезками а и b.

Задачу эту можно решить двояким путём:

1) На произвольной прямой (черт. 4) откладываем отрезки АВ = а и ВС = b; на АС, как на диаметре, описываем полуокружность; из В восставляем до пересечения с окружностью перпендикуляр BD. Этот перпендикуляр и есть искомая средняя пропорциональная между АВ и ВС.

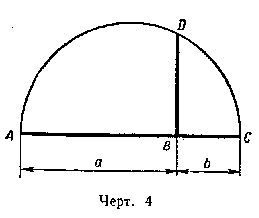
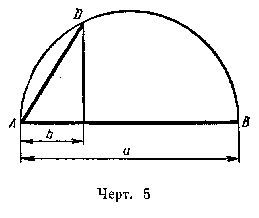
2)  На произвольной прямой (черт. 5) откладываем от точки А отрезки а и b. На большем из этих отрезков описываем полуокружность. Проведя из конца меньшего отрезка перпендикуляр к АВ до пересечения его с окружностью в точке D, соединяем А с D. Хорда AD есть средняя пропорциональная между а и b.

5. (191.) Теорема Пифагора. Доказанные выше теоремы позволяют обнаружить замечательное соотношение между сторонами любого прямоугольного треугольника. Это соотношение было впервые замечено греческим геометром Пифагором (VI в. до н. э.) и носит поэтому его имя — теорема   Пифагора.

Если стороны прямоугольного треугольника измерены одной и той же единицей, то квадрат длины  гипотенузы равен сумме квадратов длин катетов.

Пусть ABC (черт. 6) есть прямоугольный треугольник, AD — перпендикуляр, опущенный на гипотенузу из вершины прямого угла.

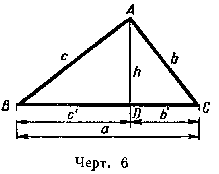
Положим, что стороны и отрезки гипотенузы измерены одной и той же единицей, причём получились числа а, b, с, с' и b' (принято длины сторон треугольника обозначать малыми буквами, соответствующими большим буквам, которыми обозначены противолежащие углы). Применяя теорему § 2 (188), можем написать пропорции:

а : с = с : с'   и  а : b = b : b',

откуда

ас' = с² и ab' = b².

Сложив  почленно  эти два  равенства,  найдём:

ас' + ab' = с² + b²,    или     а(с' + b') = с² + b².

Но с' + b' = а,  следовательно,

a² = с² + b².

Эту теорему обыкновенно выражают сокращённо так: квадрат гипотенузы равен сумме квадратов катетов.

Теорема Пифагора имеет ещё другую формулировку: площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на катетах.

Пример. Положим, что катеты, измеренные какой-нибудь линейной единицей, выражаются числами 3 и 4; тогда гипотенуза в той же единице выразится числом х, удовлетворяющим уравнению:

х²  = 3² + 4² = 9 + 16 = 25,     откуда        х = √25 = 5.

Замечание. Прямоугольный треугольник со сторонами 3, 4 и 5 называется часто египетским треугольником, так как он был известен ещё древним египтянам. Так, их землемеры для построения прямого угла на земной поверхности пользовались таким приёмов: бечёвку посредством узлов они разделяли на 12 равных частей; затем, связав концы, натягивали её на земле (посредством кольев) в виде треугольника со сторонами в 3, 4 и 5 делений; тогда угол между сторонами, равными 3 и 4, оказывался прямым¹.
_________________
 ¹ Прямоугольные треугольники, у которых стороны измеряются целыми числами, носят название пифагоровых треугольников. Можно доказать, что катеты х и у и гипотенуза z таких треугольников выражаются следующими формулами:

х = 2ab,       у = а² — b²,       z = а² + b² ,

где a и b — произвольные целые чцвяа при условии, что а > b.

6. (192.) Следствие. Квадраты катетов относятся между собой, как прилежащие отрезки гипотенузы. Действительно, из уравнений предыдущего параграфа находим:

c² : b² = ac' : ab' = с': b'.

7. (193.) Замечание.   К трём  равенствам, которые  мы  вывели выше:

1) ас' = с²;     2) ab' = b²   и    3) a² = с² + b²,

можно присоединить ещё следующие два:

4) b' + с' = а    и     5)  h² = b'с' '

(если буквой h обозначим длину высоты AD). Из этих равенств третье, как мы видели, составляет следствие первых двух и четвёртого, так что из пяти равенств только четыре независимы; вследствие этого можно по данным двум из шести чисел находить остальные четыре.

Для примера положим, что нам даны отрезки гипотенузы b' = 5 м и с' = 7 м; тогда

а = b' + с'  = 12;                             
с = √ac' = √12•7 = √84 = 9,165 ...
b = √ab' = √12•5 = √60 =  7,745 ...
 h = √b'c' = √5 • 7 = √35 =  5,916...