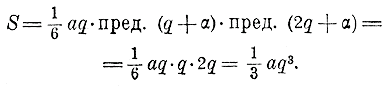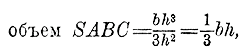ОТДЕЛ СЕМНАДЦАТЫЙ.

ПЕРВООБРАЗНАЯ ФУНКЦИЯ.

Глава первая. Нахождение  площади, ограниченной дугою параболы,ординатою и абсциссою.
Глава вторая. Первообразная функция.
Глава третья.Некоторые применения первообразной функции.

Глава первая.

Нахождение  площади, ограниченной дугою параболы,
ординатою и абсциссою.

376. Способ 1-й; посредством нахождения предела суммы бесконечно большою числа слагаемых.

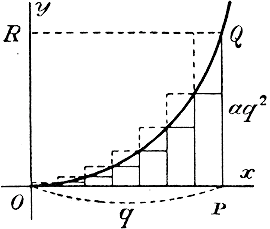
Обозначим эту ширину буквой α и площади полос (слева направо) буквами: s₁, s₂, s₃,...s_n. Построим для каждой полосы два прямоугольника, оба с общим основанием α и с высотою: у одного (выходящего), равною ординате, ограничивающей полосу справа, у другого (входящего), равною ординате, ограничивающей полосу слева. Из чертежа видно, что площадь каждой полосы меньше площади соответствующего прямоугольника выходящего, но больше площади соответствующего прямоугольника входящего. Значит:

α y₁ > s₁ > 0
α y₂ > s₂ > αy₁
α y₃ > s₃ > αy₂
................................
α y_n > s_n > α y_{n -1}

Сложив все эти неравенства, получим:

α (y₁ + y₂ +...  +  y_n) > S >α (y₁ + y₂ +...  +  y_n-1)

Разность между крайними частями последнего неравенства равна α y_n = α • PQ; поэтому

α (y₁ + y₂ +...  +  y_n) — S <  α • PQ.

Вообразим теперь, что мы неограниченно увеличиваем число n полос; тогда α —>0, поэтому и α • PQ —>0. Значит, из последнего неравенства следует, что:

S=пред. α (y₁ + y₂ +...  +  y_n), если α —>0.

Остается найти этот предел. Из уравнения параболы  у = ах² находим:

y₁ = аα²,    y₂ = а(2α)²,    y₃ = а(3α)²  ,...,   y_n = а(nα)².

Значит:

y₁ + y₂ + y₃+...  +  y_n= аα²(  1² + 2² + 3² +...+ n² ) =

(ч. I, отдел 10 глава 1§ 244) и потому

Разобьем α³ на 3 множителя: ααα; из них один отнесем к сомножителю n, другой к сомножителю n +1 и третий к сомножителю 2n +1. Тогда можем написать:

(так как αn = q). Предел произведения равен произведению пределов; поэтому:

Выражение это можно предотавить так:

Таким образом, площадь рассматриваемой фигуры составляет ¹/₃  площади прямоугольника OPQR, две стороны которого суть абсцисса и ордината, ограничивающие данную площадь; ²/₃  этого прямоугольника приходится на площадь фигуры ORQ.

377. Способ 2-й: посредством вспомогательной функции.

Решим теперь ту же задачу другим приемом, имеющим очень большое значение в математике при нахождении площадей и объемов.

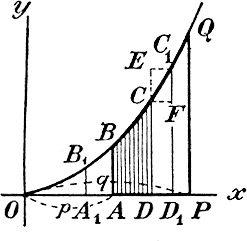
Пусть OD = x и CD = у. Очевидно, что если х изменяется, то изменяется и площадь ABCD (мы ее обозначим буквою z); значит, эта площадь есть некоторая функция от абсциссы х. Если мы эту функцию найдем, то, приняв в ней x = OP = q, мы найдем тогда и площадь ABQP, а приняв еще р = 0, получим площадь OPQ. Для нахождения этой функции предварительно разъясним следующее важное свойство ее.

Пусть x = OD получит некоторое приращение Δx = DD₁, тогда площадь z получит приращение Δz, равное площади DCC₁D₁ Площадь эта меньше площади прямоугольника DEC₁D_1, но больше площади прямоугольника DCFD₁ поэтому:

Δx • C₁D₁ > Δz > Δx • CD

откуда:

C₁D₁> ^Δz /_Δx> CD

Предположим  теперь,   что   Δz —>0.    Тогда   отношение ^Δz /_Δx стремится к пределу, называемому производной z' от функции z, a C₁D₁ имеет, очевидно, пределом CD. Значит:

z'  = пред.^Δz /_Δx = CD.

Мы приходим таким образом к следующему свойству функции z :площадь ABCD есть такая функция от переменной абсциссы х = OD, от которой производная равна переменной ординате у = CD.

В нашем примере CD = aх². Поэтому теперь возникает вопроc, нельзя ли найти такую функцию, чтобы ее производная равнялась aх². Легко сообразить, что за искомую функцию можно принять одночлен ¹/₃ ах³ , так как (¹/₃ ах³)' = ¹/₃ • 3ах^3-1 = aх². Но не только  ¹/₃ ах³ дает производную aх², та же производная получается и от функций: ¹/₃ ах³ +1,  ¹/₃ ах³ +2, ..., вообще от функции вида   ¹/₃ ах³ + C,  где С означает произвольное постоянное число (положительное или отрицательное). Дейcтвительно, так как производная от суммы равна сумме производных от слагаемых и производная от постоянного числа равна нулю, то

(¹/₃ ах³ + C)' = (¹/₃ ах³ )' + С = aх² + 0 = aх².

Значит, существует бесчисленное множество функций, от которых производная равна данной функции; все они представляют собою одну и ту же функцию (в нашем случае ¹/₃ ах³), к которой прибавлено произвольное постоянное число.

Это же видно и из чертежа 2-го. Если для функции, выражающей площадь ABCD, производная равна ординате CD, то та же самая ордината CD будет служить производной для всякой другой функции, выражающей площадь, которая получится вместо ABCD, если ординату АВ отодвинуть на произвольное расстояние влево от АВ, или вправо от АВ, напр., если вместо ABCD взять площадь A₁B₁CD. Действительно, будет ли взята площадь ABCD, или площадь A₁B₁CD, приращение Δz, соответствующее приращению абсциссы х на Δx = DD₁, остается то же самое, следовательно, и предел отношения Δz : Δx, когда Δx—> 0 будет тот же самый.

Таким образом, z =  ¹/₃ ах³ + C.  Здесь С остается произвольным, пока речь идет только о том, чтобы производная z' равнялась aх². Но в нашем вопросе  еще требуется, чтобы искомая функция при х = ОА = р обратилась в нуль. Тогда число С должно получить такое значение, которое удовлетворяет равенству: ¹/₃ аp³ + C = 0,
откуда найдем: C = — ¹/₃ аp³ . Следовательно:

z =  ¹/₃ ах³— ¹/₃ аp³

Если в этой функции положим x = OP= q, то получим:

площ. ABCD = ¹/₃ аq³— ¹/₃ аp³,

и, наконец, если еще допустим, что р = 0, то найдем:

площ. OQP = ¹/₃ аq³ = ¹/₃ аq²q= ¹/₃PQ•q,

т. е. мы получим ту же формулу, которую нашли раньше другим путем.

Глава вторая.

Первообразная функция.

378. Определение. В предыдущем параграфе нам пришлось решать вопрос: дана некоторая функция (в нашей задаче у = aх²); найти такую другую функцию, чтобы производная от нее равнялась данной функции. Функция, от которой производная равна данной функции, называется первообразной функцией по отношению к этой данной. Так, функция z = ¹/₃ ах³ + C, которую мы сейчас нашли, есть первообразная по отношению к данной функции у = aх², так как

(¹/₃ ах³ + C)'  = aх².

Очевидно, что вопрос о нахождении первообразной функции есть вопрос обратный нахождению производной от данний функции¹⁾. Решение его основывается на умeньи находить производные. Так, зная, что (kх³)' = 3 kх², мы сoображаем, что первообразная функция от kх² есть ¹/₃ kх³.

Подобно этому легко находим:

1) если z' = х, то z = ¹/₂х² + С

[проверка:  ( ¹/₂ х² + С)' = ¹/₂  2х ^2-1 = х ]

2)  если z' = 3х, то z =3• ¹/₂ х² + C = ³/₂ х² + C

3)  если z' = a х, то z = a • ¹/₂ х² + C= ¹/₂ aх²+ C;

4)  если z' = х², то z = ¹/₃ х³ + C;

"5) если z' = 3х²— 2х, то z = х³ — х²+ C;

6) если z' = ах² + bх+ c, то z = ¹/₃ aх³ + ¹/₂ bх²+ сх + С; и т. п.

Глава третья.

Некоторые применения первообразной функции.

379. Нахождение закона пространства по данному закону скорости. Мы видели (отдел 15 глава 5 § 340), что если при каком-нибудь прямолинейном движении известна функция: e = f{t), выражающая зависимость пространства е от времени t, в течение которого это пространство проходится, то производная от этой функции выразит скорость движения в зависимости от времени: f'(t) = v.Значит, по данному закону пространства мы можем найти закон скорости. Обратно, если известен закон скорости, то мы можем найти закон пространства; стоит только найти первообразную функцию от той, которая выражает закон скорости. Так, при свободном падении тела скорость, как мы знаем, подчиняется закону: v = gt; тогда высота, с которой тело падает в течение t секунд, должна быть первообразной функцией от gt, а эта функция есть  ¹/₂gt² + С. Для определения С положим t = 0; тогда высота, соответствующая этому значению времени, должна быть 0, и следовательно, С = 0, и потому высота h, проходимая падающим телом в t секунд, выражается формулою h =¹/₂gt².

Подобно этому, при движении тела, брошенного вертикально вверх с начальною скоростью v₀, скорость выражается формулою: v = v₀ — gt. Тогда высота, на которую тело подымается в t секунд, должна выразится формулою h = v₀ t — ¹/₂gt² + C, где С надо принимать равным 0, так какими t = 0 высота поднятия h также равна 0.

380. Нахождение закона скорости по данному закону ускорения. Мы видели (отдел 15 глава 5 § 343), что если известна функция, выражающая скорость в зависимости от времени: v = f (t), то производная от этой функции выразит ускорение w этого движения: w =f (t). Значит, наоборот, если известна функция, выражающая зависимость ускорения от времени, то первообразная функция выразит зависимость скорости от времени. Так, при движении тела, брошенного вертикально вверх, ускорение всегда равно — g; тогда скорость v должна быть первообразной функцией от—g, т. е. v= — gt + C. Положив t = 0, найдем: v₀ = С и, следовательно, v = — gt + v₀ = v₀— gt.

381. Применение первообразной функции к нахождению объемов. Объем пирамиды. Первообразной функцией можно пользоваться часто и при нахождении объемов. Приведем этому некоторые примеры.

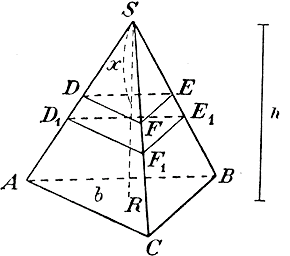
Дадим высоте х приращение Δ х, от чего тр-к DEF переместится в положение D₁E₁F₁. Тогда объем пирамиды получит приращение Δ z, равное объему слоя, заключенного между DEF и D₁E₁F₁. Очевидно, что объем этого слоя больше объема призмы, у которой основание есть тр-к DEF и высота Δ х, но меньше объема призмы, у которой основание есть тр-к D₁E₁F₁ и высота Δ х. Но объем призмы равен произведению площади основания на высоту; поэтому:

площ. D₁E₁F₁• Δ х > Δ z >площ. DEF • Δ х.

откуда:

площ. D₁E₁F₁ > ^Δz /_Δx >площ. DEF .

Положим теперь, что Δ х --> 0; тогда ^Δz /_Δx--> z' и площ. D₁E₁F₁ --> площ. DEF. Значит:

z' = площ. DEF.

Из свойства сечений пирамиды, сделанных плоскостями, параллельными основанию, следует:

площ. DEF : площ. АВС = х² : h²,

откуда:

Значит:

и поэтому:

Если  x = 0,  то   объем   пирамиды равен 0;  значит,   C = 0 и потому:

Теперь положим, что x = h,тогда найдем объем полной пирамиды:

т. е. объем треугольной пирамиды равен одной трети произведения площади основания на высоту.

Так как многоугольная пирамида есть   сумма   объемов  треугольных пирамид, то этот вывод  относится и к многоугольной пирамиде.

382. Объем  конуса определяется так же, как и объем пирамиды.

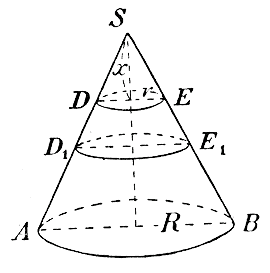
Так как объем цилиндра равен произведению площади основания на  высоту, то, значит:

площ. DE • Δ x < Δ z < пл. D₁E₁ • Δ x,

откуда:

площ. DE<  ^Δz /_Δx < пл. D₁E₁

Предположим теперь, что Δ x—> 0; тогда:

^Δz /_Δx —>z',  а   D₁E₁—> DE

Значит:

z'= площ. DE = πr ².

Из чертежа видно, что х : Н = r : R; отсюда находим:

следовательно,

При х = 0 объем z должен  равняться   также   нулю: следовательно, С = 0 и потому

Положим теперь х = Н; тогда найдем:

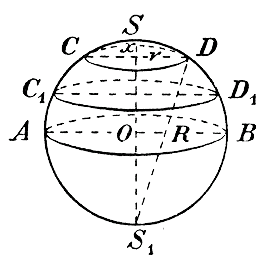
т. е. объем конуса равен одной трети произведения площади основания на высоту.

383. Объем шарового сегмента и шара.    Пусть  в   шаре   радиуса   R (черт. 5)  проведен   произвольный диаметр   SS₁   и  какою-нибудь   плоскостью  CD  перпендикулярною к этому диаметру, сделано в шаре сечение на расстоянии  х  от конца  S диаметра SS₁ Плоскость эта отсечет от шара сегмент SCD, объем которого обозначим z, а радиус основания r.

Черт. 5

Пусть х получит приращение Δ x и круг CD займет положение  C₁D₁ Тогда  объем  z получит приращение  Δ z, равное объему слоя, заключенного между кругами CD и C₁D₁ Объем этот больше объема цилиндра, c высотою Δ x и основание которого есть круг CD, но меньше объема цилиндра с тою же высотою Δ x, но с основанием C₁D₁. Следовательно,

площ. CD • Δ x < Δ z < пл. C₁D₁ • Δ x,

откуда:

площ. CD <  ^Δz /_Δx < пл. C₁D₁

Если Δ x—>0, то  ^Δz /_Δx —>z',  и  площ. C₁D₁ —> площ. CD.

Значит:

z' = площ. СD = πr ²

Если соединим точку D прямыми с S и S₁ , то получим прямоугольный треугольник DSS₁ . В этом треугольнике перпендикуляр r, опущенный из вершины прямого угла на гипотенузу, есть средняя пропорциональная величина между отрезками гипотенузы, из которых верхний есть х, а нижний 2R — х. Значит, r ² = x (2R — x) и потому:

z' = πx (2R — x) = 2πRx — πx ².

Следовательно,

z = 2πR • ¹/₂ x ² — π • ¹/₃ x ³ + С = πR x ² — ¹/₃ πx ³ + С.

Так как при x = 0 также и z =0, то и С = 0; значит:

z = πR x ² — ¹/₃ πx ³= π x ²( R — ¹/₃ x  )

Таким образом, объем шарового сегмента равен объему цилиндра, у которого радиус основания есть высота сегмента, а высота равна радиусу шара, уменьшенному на третью часть высоты сегмента.

При x = R получим объем полушария, а умножив его на 2, найдем

объем шара = πR²(R — ¹/₃ R) • 2 = ⁴/₃ πR³.

Так как ⁴/₃ πR³ = ¹/₃• 4πR² • R, то можно сказать, что объем шара равен одной трети произведения его поверхности на радиус.