ГЛАВА ПЕРВАЯ ПРЯМЫЕ И ПЛОСКОСТИ
II. ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ И ПЛОСКОСТИ
Параллельные прямые
8. Предварительное замечание. Две прямые могут быть расположены в пространстве так, что через них нельзя провести плоскость.
Возьмём, например (черт. 4), две такие прямые АВ и DЕ, из которых одна пересекает некоторую плоскость Р, а другая лежит на ней, но не проходит через точку (С) пересечения первой прямой и плоскости Р.
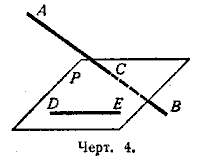
Через такие две прямые нельзя провести плоскость, потому что в противном случае через прямую и точку С проходили бы две различные плоскости: одна Р, пересекающая прямую АВ, и другая, содержащая её, а это невозможно (§ 3).
Две прямые, не лежащие в одной плоскости, конечно, не пересекаются, сколько бы их ни продолжали; однако их не называют параллельными, оставляя это название дли таких прямых, которые, находясь в одной плоскости, не пересекаются, сколько бы их ни продолжали.
Две прямые, не лежащие в одной плоскости, называются скрещивающимися.
Прямая и плоскость, параллельные между собой
9. Определение. Плоскость и прямая, не лежащая в этой плоскости, называются параллельными, если они не пересекаются, сколько бы их ни продолжали.
10. Теорема. Если прямая (АВ, черт. 5) параллельна какой-нибудь прямой (СD), расположенной в плоскости (Р), то она параллельна самой плоскости.
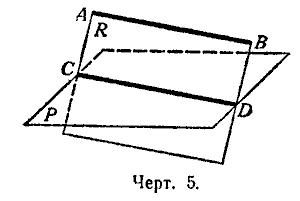
Проведём через АВ и СD плоскость R и предположим, что прямая АВ где-нибудь пересекается с плоскостью Р. Тогда точка пересечения, находясь на прямой АВ, должна принадлежать также и плоскости R, на которой лежит прямая АВ, в то же время точка пересечения, конечно, должна принадлежать и плоскости Р. Значит, точка пересечения, находясь одновременно и на плоскости R и на плоскости Р, должна лежать на прямой СD, по которой пересекаются эти плоскости; следовательно прямая АВ пересекается с прямой СD. Но это невозможно, так как по условию АВ||СD, значит, нельзя допустить, чтобы прямая АВ пересекалась с плоскостью Р, и потому АВ||Р.
11. Теорема. Если плоскость (R, черт. 5) проходит через прямую (АВ), параллельную другой плоскости (Р), и пересекает эту плоскость, то линия пересечения (СD) параллельна первой прямой (АВ).
Действительно, во-первых, прямая СD лежит в одной плоскости с прямой АВ, во-вторых, эта прямая не может пересечься с прямой АВ, потому что в противном случае прямая АВ пересекалась бы с плоскостью Р, что невозможно.
12. Следствие 1. Если прямая (АВ, черт. 6) параллельна каждой из двух пересекающихся плоскостей (Р и Q), то она параллельна линии их пересечения (СD).
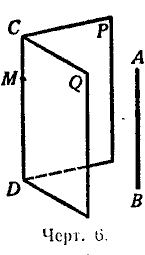
Проведём плоскость через АВ и какую-нибудь точку М прямой СD. Эта плоскость должна пересечься с плоскостями Р и Q по прямым, параллельным АВ и проходящим через точку М. Но через точку М можно провести только одну прямую, параллельную АВ; значит, две линии пересечения проведённой плоскости с плоскостями Р и Q должны слиться в одну прямую. Эта прямая, находясь одновременно на плоскости Р и на плоскости Q, должна совпадать с прямой СD, по которой плоскости Р и Q, пересекаются; значит, СD || AВ.
13. Следствие 2. Если две прямые (АВ и СD, черт. 7) параллельны третьей прямой
(ЕF), то они параллельны между собой.
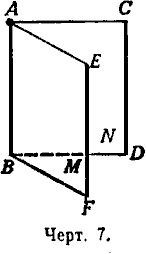
Проведём плоскость М через параллельные прямые АВ и ЕF. Так как СD||EF, то
СD||M (§ 10).
Проведём также плоскость N через СD в некоторую точку А прямой AВ.
Так как EF||СD, то EF||N. Значит, плоскость N должна пересечься с плоскостью M по прямой, параллельной EF (§ 11) и в то же время проходящей через точку А. Но в плоскости М через А проходит единственная прямая, параллельная EF, именно прямая АВ. Следовательно, плоскость N пересекается с М по прямой АВ; значит, СD || AВ.
14. Определение. Две плоскости называются параллельными, если они не пересекаются, сколько бы их ни продолжали.
15. Теорема. Если две пересекающиеся прямые (АВ и АС, черт. 8) одной плоскости
(Р) соответственно параллельны двум прямым (А1В1 и А1С1) другой плоскости (Q), то эти плоскости параллельны.
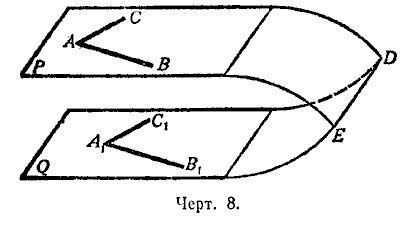
Прямые АВ и АС параллельны плоскости Q (§10).
Допустим, что плоскости Р и Q пересекаются по некоторой прямой DE (черт. 8). В таком случае AB||DE и AC||DE (§11). Таким образом, в плоскости Р через точку А проходят две прямые АВ и АС, параллельные прямой DE, что невозможно. Значит, плоскости Р и Q не пересекаются.
16. Теорема. Если две параллельные плоскостu (Р и Q черт. 9) пересекаются третьей плоскостью (R), то линии пересечения (АВ и СD) параллельны.
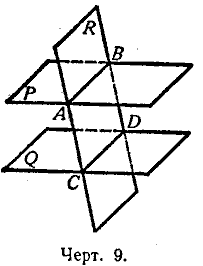
Действительно, во-первых, прямые АВ и СD находятся в одной плоскости (R); во-вторых, они не могут пересечься, так как в противном cлучае пересекались бы плоскости Р и Q, что противоречит условию.
17. Теорема. Отрезкu параллельных прямых (АС и ВD черт. 9), заключённые между параллельными плоскостями (Р и Q), равны.
Через параллельные прямые АС и ВD проведём плоскость R; она пересечёт плоскости Р и Q по параллельным прямым АВ и СD следовательно, фигура АВDС есть параллелограмм, и потому АС||ВD.
18. Теорема. Два угла (ВАС и В1А1С1, черт. 10) с соответственно параллельными и одинаково направленными сторонами равны и лежат в параллельных плоскостях (Р и Q).
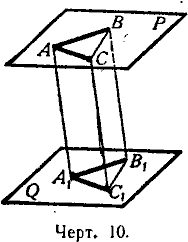
Что плоскости Р и Q параллельны, было доказано выше (§ 15); остаётся доказать, что углы А и А1 равны.
Отложим на сторонах углов произвольные, но равные отрезки АВ = А1В1; АС = А1С1 и проведём прямые АА1, ВВ1, СС1, ВС и В1C1.
Так как отрезки АВ и А1В1 равны и параллельны, то фигура АВВ1А1 есть параллелограмм; поэтому отрезки АА1 и ВВ1 равны и параллельны. По той же причине равны и параллельны отрезки АА1 и СС1, следовательно, ВВ1||СС1 и ВВ1= СС1.
Поэтому ВС = В1С1 и /\ АВС = /\ А1В1С1 (по трём сторонам); значит, /
А = /
А1
19. Через точку (А, черт. 11), расположенную вне данной прямoй (а), в пространстве провести прямую, параллельную данной прямой (а).
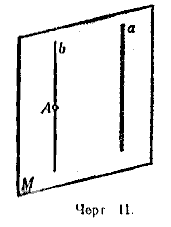
Решение. Через прямую а и точку А проводим плоскость М. В этой плоскости строим прямую b, параллельную прямой а.
Задача имеет единственное решение. В самом деле, искомая прямая должна лежать с прямой а в одной плрскости. В этой же плоскости должна находиться точка А, через которую проходит искомая прямая. Значит, эта плоскость должна совпадать с M. Но в плоскости М через точку А можно провести только одну прямую, параллельную прямой а.
20. Через данную точку (А, черт. 12) провести плоскость, параллельную данной плоскости (Р), не проходящей через точку А.
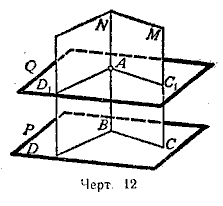
Решение. Проводим на плоскости Р через какую-либо точку В две какие-либо прямые ВС и ВD. Построим две вспомогательные плоскости: плоскость М—через точку А и прямую ВС и плоскость N—через точку А и прямую ВD. Искомая плоскость, параллельная плоскости Р, должна пересечь плоскость М по прямой, параллельной BС, a плоскость N — по прямой, параллельной ВD (§ 16).
Отсюда вытекает такое построение:
через точку А проводим в плоскости М прямую АС1 ||ВС, а в плоскости N прямую
АD1 ||ВD.
Через прямые АС1 и АD1 проводим плоскость Q. Она и будет искомой. В самом деле, стороны угла D1АС1 расположенного в плоскости Q параллельны сторонам угла DВС, расположенного в плоскости P. Следовательно, Q|| Р.
Так как в плоскости М через точку А можно провести лишь одну прямую, параллельную ВС, а в плоскости N через точку А лишь одну прямую, параллельную BD, то задача имеет единственное решение. Следовательно, через каждую точку пространства можно провести единственную плоскость, параллельную данной плоскости.
21. Через данную прямую (а, черт. 13) провести плоскость, параллельную другой данной прямой (b).
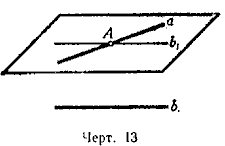
Решение. 1-й случай. Прямые а и b не параллельны.
Через какую нибудь точку А прямой а проводим прямую b1, параллельную b ; через прямые а и b1 проводим плоскость. Она и будет искомой (§10). Задача имеет в этом случае единственное решение.
2-й случай. Прямые а и b параллельны. В этом случае задача неопределенна: всякая плоскость, проходящая через прямую а, будет параллельна прямой b.
22. Пример более сложной задачи иа построение. Даны две скрещивающиеся прямые (а и b, черт. 14) и точка А, не лежащая ни на одной из данных прямых. Провести через точку А прямую, пересекающую обе данные прямые (а и b).
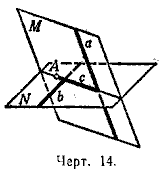
Решение. Так как искомая прямая должна проходить через точку А и пересекать прямую а, то она должна лежать в плоскости, проходящей через прямую а и точку А (так как две её точки должны лежать в этой плоскости: точка А и точка пересечения с прямой а). Совершенно так же убеждаемся, что искомая прямая должна лежать в плоскости, проходящей через точку А и прямую b . Следовательно, она должна служить линией пересечения этих двух плоскостей. Отсюда такое построение.
Через точку А и прямую а проводим плоскость М; через точку А и прямую b проводим плоскость N. Берем прямую с пересечения плоскостей М и N. Если прямая с не параллельна ни одной из данных прямых, то она пересечётся с каждой из данных прямых (так как с каждой из них она лежит в одной плоскости: а и с лежат в плоскости М,
b и с — в плоскости N). Прямая с будет в этом случае искомой.
Если же а || с или b||с, то задача не имеет решения.