ГЛАВА ПЕРВАЯ ПРЯМЫЕ И ПЛОСКОСТИ

V. ДВУГРАННЫЕ УГЛЫ, УГОЛ ПРЯМОЙ С ПЛОСКОСТЬЮ,
УГОЛ ДВУХ СКРЕЩИВАЮЩИХСЯ ПРЯМЫХ, МНОГОГРАННЫЕ УГЛЫ

Перпендикулярные плоскости

42. Определение. Две плоскости называются взаимно перпендикулярными, если, пересекаясь, они образуют прямые двугранные углы.

43.Теoрема (выражающая признак перпендикулярности двух  плоскостей). Если  плоскость (Р,  черт.  31) проходит через перпендикуляр (АВ) к другой  плоскости (Q), то она перпендикулярна к этой плоскости.

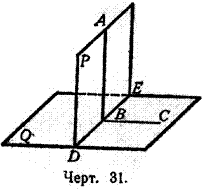
Пусть DE будет линия пересечения плоскостей Р и Q. На плоскости Q проведем
ВС _|_ DE. Тогда угол ABC будет линейным углом двугранного угла PDEQ.

Так как прямая АВ по условию перпендикулярна к Q, то АВ _|_ ВС; значит, угол АВС прямой, а потому и двугранный угол прямой, т. е. плоскость Р перпендикулярна к плоскости Q.

44. Теорема. Если две плоскости (Р и Q, черт. 31) взаимно перпендикулярны и к одной из них (к Q) проведён перпендикуляр (АВ), имеющий общую точку (А) с другой плоскостью (Р), то этот перпендикуляр весь лежит в этой плоскости (Р).

Предположим, что перпендикуляр АВ не лежит в плоскости Р (как изображено на черт. 32).

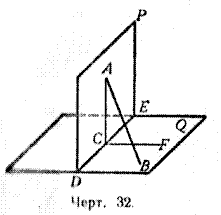
Пусть DE будет линия пересечения плоскостей Р и Q. На плоскости Р проведём прямую AC _|_ DE, а на плоскости Q проведём прямую CF _|_ DE. Тогда угол ACF, как линейный угол прямого двугранного угла, будет прямой. Поэтому линия АС, образуя прямые углы с DE и CF, будет перпендикуляром к плоскости Q. Мы будем иметь тогда два  перпендикуляра, опущенные из одной и той же точки А на плоскость Q, именно АВ и АС. Так как это невозможно (§ 36), то допущение неверно; значит, перпендикуляр АВ лежит в плоскости Р.

45. Следствие. Линия пересечения АВ (черт. 33) двух плоскостей (Р и Q), перпендикулярных к третьей плоскости (R), есть перпендикуляр к этой плоскости.

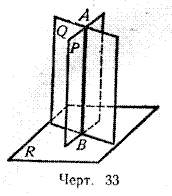
Действительно, если через какую-нибудь точку А линии пересечения плоскостей Р и Q проведём перпендикуляр к плоскости R, то этот перпендикуляр согласно предыдущей теореме должен лежать и в плоскости Q, и в плоскости Р, значит, он сольётся с АВ.

Угол двух скрещивающихся прямых

46. Определение. Углом двух скрещивающихся прямых {АВ и CD, черт. 34), для которых дано положение и направление, называется угол (MON), который получится, если из произвольной точки пространства (О) проведём полупрямые (ОМ и ON), соответственно параллельные данным прямым (АВ и CD) и одинаково с ними направленные.

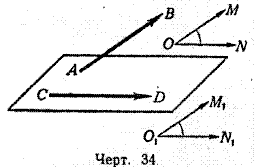
Величина этого угла не зависит от положения точки О, так как если построим указанным путём угол М₁O₁N₁ с вершиной в  какой-нибудь другой точке О₁,
то / MON = /  М₁O₁N₁, потому что эти углы имеют соответственно  параллельные и одинаково направленные стороны.

Угол, образуемый прямой с плоскостью

47. Проекция точки и прямой на плоскость. Мы говорили ранее (§ 25), что когда из одной точки проведены к плоскости перпендикуляр и наклонная, то проекцией этой наклонной на плоскость называется отрезок, соединяющий основание перпендикуляра с основанием наклонной. Дадим теперь более общее определение проекции.

1) Ортогональной (или прямоугольной) проекцией какой-нибудь точки на данную плоскость (например, точки M на плоскость Р, черт. 35) называется основание (m) перпендикуляра, опущенного на эту плоскость из взятой точки.

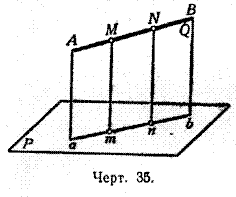
2) Ортогональной проекцией какой-нибудь линии на плоскость называется геометрическое место проекций всех точек этой линии.

В частности, если проектируемая линия есть прямая (например, АВ, черт. 35), не перпендикулярная к плоскости (Р), то проекция её на эту плоскость есть также прямая. В самом деле, если мы через прямую АВ и перпендикуляр Мт, опущенный на плоскость проекций из какой-нибудь одной точки М этой прямой, проведём плоскость Q, то эта плоскость должна быть перпендикулярна к плоскости Р; поэтому перпендикуляр, опущенный на плоскость P из любой точки прямой АВ (например, из точки М), должен лежать в этой плоскости Q (§ 44) и, следовательно, проекции всех точек прямой АВ должны лежать на прямой аb, по которой пересекаются плоскости Р и Q.
Обратно, всякая точка этой прямой аb есть проекция какой-нибудь точки прямой АВ, так как перпендикуляр, восставленный из любой точки прямой аb, лежит на плоскости следовательно, пересекается с АВ в некоторой точке. Таким образом, прямая аb представляет собой геометрическое место проекций всех точек данной прямой АВ и, следовательно, есть её проекция.

Для краткости речи вместо „ортогональная проекция" мы будем говорить просто „проекция".

48. Угол прямой с плоскостью. Углом прямой (АВ, черт. 36) с плоскостью (Р) в том случае, когда прямая наклонна к плоскости, называется острый угол (ABC), составленный этой прямой с ee проекцией на плоскость.

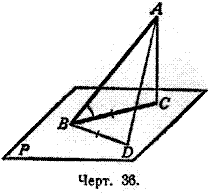
Угол этот обладает тем свойством, что он есть наименьший из всех углов, которые наклонная образует с прямыми, проведёнными на плоскости P через основание наклонной.

Докажем, например, что угол ABC меньше угла ABD.
Для этого отложим отрезок BD = ВС и соединим D с А. У треугольников ABC и ABD две стороны одного равны соответственно двум сторонам другого, но третьи стороны не равны, а именно: AD > АС (§ 26). Вследствие этого угол ABD больше угла ABC.