ГЛАВА ВТОРАЯ

ОРТОГОНАЛЬНЫЕ ПРОЕКЦИИ ТОЧКИ, ОТРЕЗКА И ФИГУРЫ

54. Изображение точки при помощи проекции на две плоскости. Вообразим плоскости проекций, горизонтальную Н и вертикальную V, пересекающиеся под прямым углом по прямой ху, которую мы будем называть осью проекций (черт. 44).

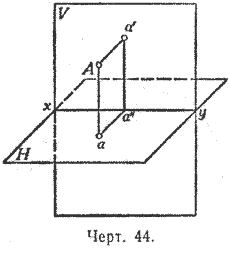
Плоскости эти образуют четыре двугранных угла, из которых мы для простоты будем рассматривать только один, именно передний верхний. Положим, что внутри этого угла расположена какая-нибудь точка А. Опустим из неё перпендикуляры на плоскости Н и V. Тогда мы получим на этих плоскостях проекции точки А, именно: а есть горизонтальная проекция, а'— вертикальная (проекции эти называются ортогональными, так как они получаются опусканием перпендикуляра на плоскость).

Обыкновенно каждая из этих проекций обозначается малой буквой одного наименования с той большой буквой, которая обозначает проектируемую точку, причём буква, обозначающая вертикальную проекцию, берётся со знаком наверху. Перпендикуляры, с помощью которых получаются проекции точки, называются проектирующими перпендикулярами: Аа — горизонтально-проектирующий перпендикуляр, Аа' — вертикально-проектирующий перпендикуляр.

Если через эти перпендикуляры проведём плоскость, то она должна быть перпендикулярной к плоскости Н и к плоскости V (§ 43); следовательно, должна быть перпендикулярна и к оси ху (§ 45), и потому прямые аа" и а'а", по которым эта плоскость пересекается с плоскостями Н и V, будут перпендикулярны к оси ху; следовательно, они образуют линейный угол двугранного угла, составленного плоскостями Н и V, а так как этот двугранный угол прямой, то и линейный его угол должен быть прямым. Таким образом, четырёхугольник Ааа''а' будет прямоугольником, плоскость которого перпендикулярна к оси ху.

Заметив это, повернём горизонтальную полуплоскость Н вокруг оси ху на 90° книзу; тогда она совпадёт с нижней вертикальной полуплоскостью, образуя с верхней вертикальной полуплоскостью одну вертикальную плоскость. При этом точки а" и а' останутся на своих местах, а точка а займёт положение ниже оси ху и расположится на продолжении перпендикуляра а' а" на расстоянии а"а, равном Аа'. Мы получим тогда развёрнутый чертёж 45, который впредь будем называть эпюром; чертёж этот состоит из прямой ху, изображающей ось проекций, и двух точек, расположенных на одном перпендикуляре к оси ху; нижняя точка есть горизонтальная  проекция,  а  верхняя — вертикальная проекция  точки  А.

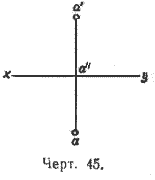
Конечно, всякой точке А, взятой внутри двугранного угла (черт. 44), соответствуют на эпюре две вполне определённые точки а и а', расположенные на одном перпендикуляре к оси ху. Обратно, всяким двум точкам эпюра а и а', расположенным на одном перпендикуляре к оси ху (точка а ниже ху, а точка а' выше ху), соответствует одна определённая точка А внутри двугранного угла. Чтобы получить эту точку, мы должны вообразить, что нижняя половина эпюра вращением вокруг оси ху снова повёрнута на 90° кверху и затем из точек а и а' восставлены перпендикуляры к плоскостям образовавшегося двугранного угла; пересечение этих перпендикуляров и определит точку А.

55. Частные случаи.

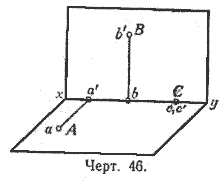
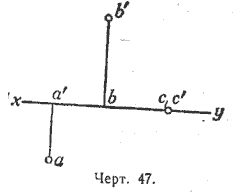
Из чертежей 46 и 47 видно, что если:

1) точка А лежит на горизонтальной плоскости, то её вертикальная проекция а' лежит на оси ху, а горизонтальная совпадает с самой точкой;

2) точка В расположена на вертикальной плоскости, то её горизонтальная проекция лежит на оси ху, а вертикальная совпадает с самой точкой;

3) точка С лежит на оси ху, то обе её проекции совпадают с самой точкой.

56. Изображение прямой. Мы уже видели (§ 47), что если проектируемая линия прямая, то и проекция ее должна быть прямой линией. Значит, отрезок прямой, соединяющей точки А и В (черт. 48), изобразится на эпюре (черт. 49) отрезками ab и а'b', из которых первый есть горизонтальная проекция, а второй — вертикальная проекция отрезка АВ. Таким образом, чтобы получить проекцию неограниченной прямой на какую-нибудь плоскость, достаточно найти проекцию на эту плоскость двух еe точек и через эти проекции провести прямую.

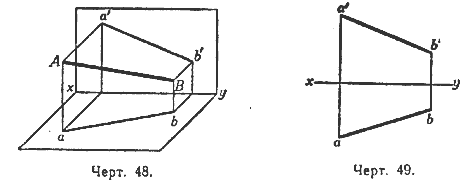
Проекции прямой можно получить ещё иначе, а именно: мы можем провести через эту прямую две плоскости: одну — перпендикулярную к горизонтальной плоскости проекций (она называется горизонтально-проектирующей плоскостью) и другую—перпендикулярную к вертикальной плоскости проекций (она называется  вертикально-проектирующей плоскостью). Пересечение этих плоскостей с плоскостями проекции даст проекции ab и а'b'.

Заметим, что если отрезок прямой обозначен буквами АВ, то его проекции обозначаются аb (горизонтальная) и а'b' (вертикальная); если неограниченная прямая обозначена одной буквой, например К, то проекции её обозначаются тоже одной буквой (малой) k (горизонтальная) и k' (вертикальная).

57. Частные случаи.

1) Один конец отрезка АВ лежит на горизонтальной плоскости.

2) Один конец отрезка СD лежит на вертикальной плоскости.

3) Отрезок EF упирается своими концами в плоскости проекции.

Эти три случая изображены в перспективном виде на чертеже 50 и проекциями на эпюре на чертеже 51.

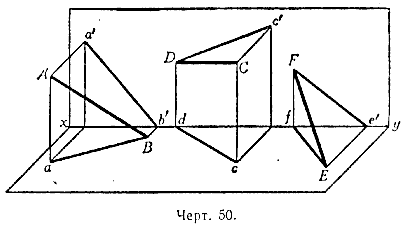
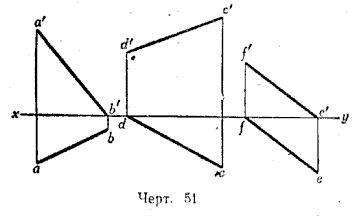
4) Отрезок АВ перпендикулярен к вертикальной плоскости проекций и упирается в неё (черт. 52 и 53).

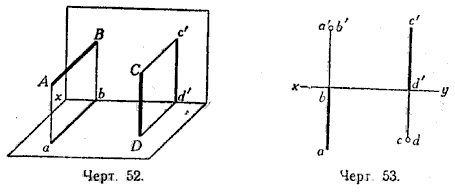
5) Отрезок СD перпендикулярен к горизонтальной плоскости и упирается в неё (черт. 52 и 53).

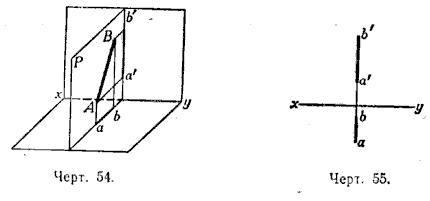
6) Отрезок АВ лежит в некоторой плоскости Р, перпендикулярной к оси ху. Тогда обе проектирующие плоскости совпадают с плоскостью Р и потому на эпюре аb, а'b' расположены на одном перпендикуляре к оси ху (черт. 54 и 55).

7) Отрезок АВ параллелен вертикальной плоскости. Тогда его горизонтальная проекция параллельна оси ху (черт. 56 и 57), а вертикальная проекция равна и параллельна АВ.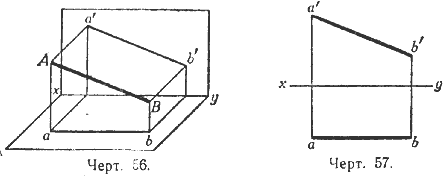

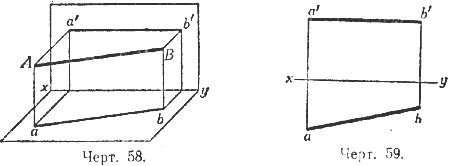
8) Отрезок АВ параллелен горизонтальной плоскости (черт. 58 и 59); тогда его вертикальная проекция параллельна оси ху, а горизонтальная  проекция  равна  и  параллельна   самому   отрезку  АВ.

58. Проекция пересекающихся прямых. Очевидно, что если две прямые (К и L) пересекаются, то пересекаются также и их одноимённые проекции (черт. 60), причём точки пересечения m и m' лежат на одном перпендикуляре к оси ху.

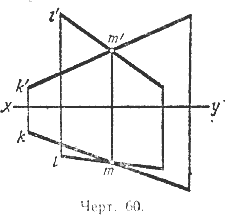
Обратно, если одноимённые проекции двух прямых пересекаются, причём точки пересечения лежат на одном перпендикуляре к оси ху, то и сами прямые пересекаются, таккак точка (m , m' ), определяемая точками пересечения проекций, принадлежит обеим прямым.

59. Проекции параллельных прямых параллельны.

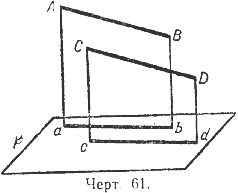
Действительно, если АВ || СD  (черт. 61), то стороны углов ВАа и DСс параллельны и потому проектирующие плоскости также параллельны (§ 15), а параллельные плоскости пересекаются третьей плоскостью (Р) по параллельным прямым (аb и cd) (§ 16).

60. Изображениями прямых с помощью двух её проекций на два взаимно перпендикулярные плоскости можно пользоваться для решения различных задач, касающихся положения прямых в пространстве.

Рассмотрим несколько примеров таких задач.

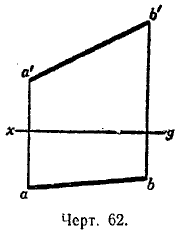
Задача 1. На эпюре даны проекции аb  и а'b'  некоторого отрезка АВ (черт. 62). Определить действительную величину этого отрезкa.

Первый способ решения. Чтобы легче было вообразить положение отрезка в пространстве, возьмём перспективное изображение отрезка АВ и его горизонтальной проекции ab (черт. 63), т. е. такое изображение, которым мы пользовались в первой главе.

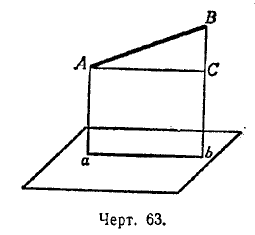
Четырёхугольник АВbа представляет собой прямоугольную трапецию с прямыми углами при точках а и b. Проведя в этой трапеции прямую АС, параллельную ab, получим прямоугольный треугольник ABC.

В этом треугольнике отрезок АВ является гипотенузой, катет АС, очевидно, равен горизонтальной проекции ab отрезка АВ. Эта проекция на эпюре задана. Катет ВС равен разности отрезков Вb и Аа.

Отрезки Вb и Аа на эпюре также даны; именно они равны соответственно расстояниям точек b' и а' от оси ху, следовательно, и разность их также можно найти на эпюре. Она равна разности расстояний точек b' и а' от оси ху.

Отсюда следует: чтобы найти действительную длину отрезка АВ, нужно построить прямоугольный треугольник, одним из катетов которого служит горизонтальная проекция ab искомого отрезка, а другим — отрезок, равный разности расстояний вертикальных проекций a' и b'  концов отрезка от оси ху. Гипотенуза этого треугольника и даёт действительную длину отрезка АВ.

Второй способ. Представим себе, что отрезок АВ в пространстве неизменно скреплён с прямой Аа, и будем вращать отрезок АВ около этой прямой до тех пор, пока он не станет параллелен вертикальной плоскости проекций (черт. 64).

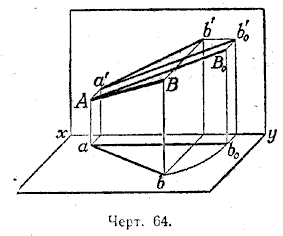
При этом его вертикальная проекция будет давать его действительную длину.

При таком вращении отрезка АВ его проекции аb и а'b' на эпюре будут меняться. Но его угол наклона к прямой Аа не будет меняться, а следовательно, не будет меняться и длина его горизонтальной проекции (меняется только её направление). Значит, при этом вращении отрезка его горизонтальная проекция изменится так, что точка а на эпюре остаётся неподвижной, а точка b перемещается по дуге окружности. Когда отрезок АВ станет параллелен вертикальной плоскости, его горизонтальная проекция сделается параллельной оси ху. Вертикальная проекция а'b'  при вращении также меняется, но так как расстояние точки В от горизонтальной плоскости остаётся неизменным, то расстояние точки b'  от оси ху также не будет меняться. Отсюда следует, что точка b'  будет.перемещаться по прямой, параллельной оси ху. Из сказанного следует, что можно получить на эпюре проекции отрезка АВ, после его поворота вокруг оси Аа, с помощью следующего построения (черт. 65):

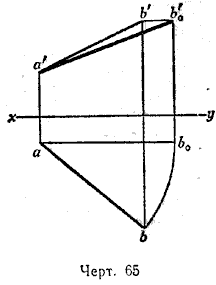
описываем дугу окружности с центром в точке а радиусом, равным аb, и находим точку её пересечения b₀ с прямой, параллельной оси ху и проходящей через точку а;
через b' проводим прямую, параллельную оси ху, и продолжаем её до пересечения в некоторой точке b'₀ с перпендикуляром к оси ху, проведённым через точку b₀.
Отрезки аb₀ и а'b'₀  будут проекциями отрезка АВ после поворота. Его вертикальная проекция а'b'₀  будет при этом давать действительную длину отрезка АВ.

61. Задача 2. На эпюре даны проекции l и l' некоторой прямой (черт. 66). Найти точки пересечения этой прямой с плоскостями проекций (эти точки называются следами прямой на плоскостях проекций).

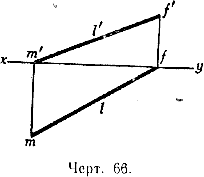
Решение. Точка встречи данной прямой с вертикальной плоскостью имеет своей горизонтальной проекцией точку на оси ху. С другой стороны, горизонтальная проекция этой точки должна лежать на прямой l. Следовательно, для нахождения на эпюре вертикального следа прямой продолжаем её горизонтальную проекцию l до встречи в точке   f с осью ху. Точка  f будет горизонтальной проекцией искомого вертикального следа. Чтобы найти его вертикальную проекцию, восставим в точке f  перпендикуляр к оси   ху и продолжим его до пересечения в точке f ' с прямой l' . Эта точка f ' и будет искомой вертикальной проекцией вертикального следа, она, очевидно, совпадает с самим вертикальным следом. Таким же путём найдём и горизонтальный след прямой: продолжаем l'  до встречи в точке т' с осью ху, в точке т' восставляем перпендикуляр к оси ху до встречи в точке т с прямой l; точка т искомая.

62. Проекция треугольника. Если в пространстве дан треугольник, то можно построить горизонтальные и вертикальные проекции его вершин и сторон. На эпюре получается, таким образом, два треугольника, которые служат горизонтальной и вертикальной проекциями данного треугольника в пространстве.

Если форма и положение треугольника в пространстве не указаны заранее, то проекции его вершин можно задавать произвольно, соблюдая лишь условие, чтобы вертикальная и горизонтальная проекции одной и той же вершины лежали на одном перпендикуляре к оси ху. Действительно, положение плоскости в пространстве вполне определяется положением трёх её точек, которые можно брать в пространстве совершенно произвольно, лишь бы они не располагались на одной прямой.

На чертеже 67 представлены проекции некоторого треугольника ABC. Пользуясь этими проекциями, можно на эпюре решать различные задачи, касающиеся положения треугольника в пространстве.

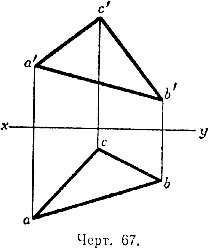
63. Задача 1. Даны проекции abc и a'b'c' треугольника (черт. 68). Построить на эпюре вертикальную проекцию прямой, лежащей в плоскости этого треугольника, горизонтальная проекция которой задана.

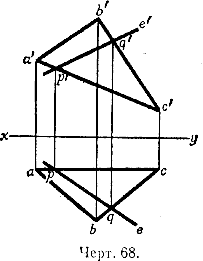
Решение. Пусть прямая е есть заданная горизонтальная проекция, она встречает прямые ас и bс соответственно в точках р и q.

Так как эта прямая проведена в плоскости треугольника ABC, то она пересекается со сторонами АС и ВС в точках, для которых р и q служат горизонтальными проекциями. Для получения вертикальных проекций тех же точек, очевидно, следует из точек р и q опустить перпендикуляры на ось ху и продолжить их до встречи в точках р' и q' соответственно с прямыми а'с' и b'с'. Прямая p'q' есть искомая вертикальная проекция прямой, лежащей в плоскости данного треугольника.

64. Задача 2. На эпюре даны проекции abc и а'b'с' треугольника ABC (черт. 69). Кроме того, дана горизонтальная проекция d точки D, лежащей в плоскости этого треугольника. Построить вертикальную проекцию этой точки.

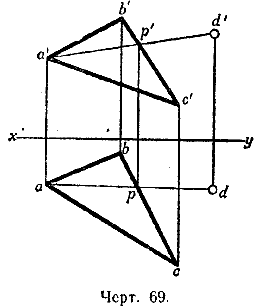
Решение. Соединив точки d и а, мы получим горизонтальную проекцию ad прямой, лежащей в плоскости треугольника ABC и соединяющей точку D с вершиной А (черт. 70).

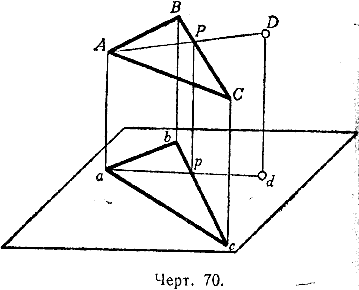
Точка р, в которой прямая ad встречает bс, есть горизонтальная проекция точки пересечения Р прямой AD со стороной ВС (черт. 70).

На прямой b'с' находим вертикальную проекцию р' той же точки, опустив из р перпендикуляр на ось. Далее, проводим прямую а'р' и на ней таким же способом находим искомую вертикальную проекцию d' точки D (черт. 69).

65. Проекция многоугольников. При построении проекций многоугольника уже нельзя произвольно задавать проекции его вершин. Если взять произвольные горизонтальные проекции вершин многоугольника, то из вертикальных их проекций произвольно (но на одном перпендикуляре с соответствующими горизонтальными проекциями) можно взять только три. Действительно, эти три вертикальные проекции вместе с горизонтальными вполне определяют плоскость, в которой лeжит многоугольник.

Поэтому вертикальные проекции остальных вершин следует брать так, чтобы они служили проекциями точек, лежащих в этой плоскости.

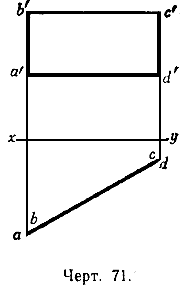
На чертеже 71 даны проекции прямоугольника, лежащего в плоскости, перпендикулярной к горизонтальной плоскости проекции, имеющего две вертикальные стороны.

На чертеже 72 представлено построение проекций шестиугольника, причём горизонтальные проекции   а, b, с, d, е, f   его вершин взяты произвольно.

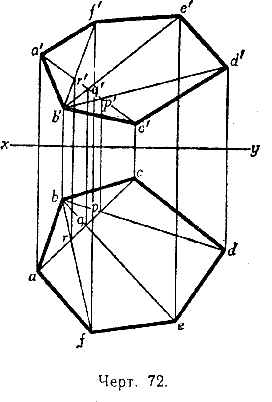
Вертикальные проекции а', b', с' выбраны на перпендикулярах к оси проекций, проведённых через точки а, b, с. При этом точку а' можно брать где угодно на перпендикуляре к оси проекций, проведённом через а, точку b' — где угодив на перпендикуляре к оси, проведённом  через b, и точку с' — где угодно на перпендикуляре к оси, проведённом через с. Вертикальные проекции остальных вершин можно построить, применяя способ, указанный в § 64. Соединив точки а, b и с, получим горизонтальные проекции двух сторон шестиугольника (аb и bс) и одной его диагонали (ас). Соединив точки а', b' и с', получим вертикальные проекции тех же сторон (а'b' и b'с') и той же диагонали (а'с'). Соединим после этого точку b с горизонтальными проекциями d, е и f остальных вершин шестиугольника. Точки пересечения прямых bd, bе и bf с прямой ас обозначим соответственно через р, q и r. Проведя через точки р, q и r прямые, перпендикулярные к оси проекций, продолжим их до пересечения с прямой а' с', тогда мы получим на этой прямой вертикальные проекции р, q и r точек пересечения трёх диагоналей шестиугольника с четвёртой, для которой вертикальной проекцией служит прямая а'с'. Вертикальные проекции этих трёх диагоналей мы получим, соединяя точки р', q' и r' с точкой b. Если теперь продолжить прямую b'р', а через точку d провести прямую, перпендикулярную к оси проекций, до пересечения с прямой b'р', то точка пересечения этих прямых d' будет служить вертикальной проекцией четвёртой вершины шестиугольника. Таким же образом, продолжая прямые b'q' и b'r' и опуская из точек е и f перпендикуляры на ось проекций, найдём вертикальные проекции е' и f' пятой и шестой вершин шестиугольника. Соединив последовательно точки а', b', с', d', е',  f' , получим искомую вертикальную проекцию шестиугольника.

66. Замечание. Метод изображения фигур и тел в ортогональных проекциях на две плоскости был разработан французским учёным Гаспаром Монжем (1745—1818). Гаспар Монж был крупнейшим французским геометром конца XVIII и начала XIX в. Во время французской революции был одним из основателей знаменитой политехнической школы, созданной конвентом. Метод Монжа в настоящее время является одним из основных в той области геометрии, которая разрабатывает методы изображения геометрических тел на плоскости и носит название начертательной геометрии. Метод Монжа имеет широкое применение в технике при вычерчивании проектов сооружений, планов зданий, частей и деталей машин и т. д. При этом методе построения на эпюре выполняются иногда по сложным правилам, пользоваться которыми можно, лишь хорошо усвоив главные факты и предложения стереометрии. Поэтому в учебниках геометрии, как и в настоящей книге, при изображении геометрических фигур и тел применяются упрощённые рисунки.

Эти рисунки представляют собой проекции изучаемых фигур, но не на две плоскости, а лишь на одну, именно на плоскость чертежа.

Как следует из всего предыдущего, одна такая проекция ещё не определяет ни положения фигуры в пространстве, ни её точных размеров, но oна даёт ясное представление о виде изучаемой фигуры. Этого представления достаточно, чтобы, основываясь на общих теоремах стереометрии, изучать свойства геометрических фигур и тел.