ГЛАВА ТРЕТЬЯ
МНОГОГРАННИКИ
IV. ПОНЯТИЕ О ПРАВИЛЬНЫХ МНОГОГРАННИКАХ
Многогранник называется правильным, если все его грани —равные правильные многоугольники и все многогранные углы равны (таков, например, куб). Из этого определения следует, что в правильных многогранниках равны все плоские углы, все двугранные углы и все рёбра.
97. Перечисление правильных многогранников. Примем во внимание, что в многогранном угле наименьшее число граней три и что сумма плоских углов выпуклого многогранного угла меньше 4d (§ 51).
Каждый угол правильного треугольника равен 2/3 d. Если повторим 2/3 d слагаемыми 3, 4 и 5 раз, то получим суммы, меньшие 4d, а если повторим 2/3 d слагаемыми 6 раз или более, то получим в сумме 4d или более. Поэтому из плоских углов, равных углам правильного треугольника, можно образовать выпуклые многогранные углы только трёх видов: трёхгранные, четырёхгранные и пятигранные.
Следовательно, если гранями правильного многогранника служат правильные треугольники, то в вершине многогранника могут сходиться или 3 ребра, или 4 ребра, или 5 рёбер. Соответственно с этим имеется три вида правильных многогранников с треугольными гранями:
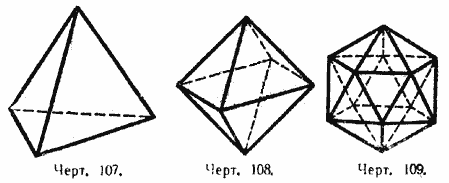
1) Правильный четырёхгранник, или тетраэдр, поверхность которого составлена из четырёх правильных треугольников (черт. 107). Он имеет 4 грани, 4 вершины и 6 рёбер.
2) Правильный восьмигранник, или октаэдр, поверхность которого составлена из восьми правильных треугольников (черт. 108). Он имеет 8 граней, 6 вершин и 12 рёбер.
3) Правильный 20-гранник, или икосаэдр, образованный двадцатью правильными треугольниками (черт. 109). Он имеет 20 граней, 12 вершин и 30 рёбер.
Угол квадрата равен d, а угол правильного пятиугольника равен 6/5 d; повторяя эти углы слагаемыми 3 раза, получаем суммы, меньшие 4d, а повторяя их 4 раза или более, получаем 4d или более. Поэтому из плоских углов, равных углам квадрата или правильного пятиугольника, можно образовать только трёхгранные углы.
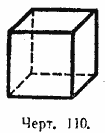
А поэтому если гранями многогранника служат квадраты, то в каждой вершине могут сходиться лишь 3 ребра. Имеется единственный правильный многогранник этого рода — это правильный шестигранник, или гексаэдр, или куб (черт. 110). Он имеет 6 граней, 8 вершин и 12 рёбер.
Если гранями правильного многогранника служат правильные пятиугольники, то в каждой вершине могут сходиться лишь 3 ребра.
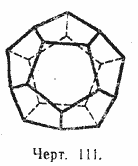
Существует единственный правильный многогранник этого рода — правильный 12-гранник, или додекаэдр. Он имеет 12 граней, 20 вершин и 30 рёбер (черт. 111).
Угол правильного шестиугольника равен 4/3 d, поэтому из таких углов нельзя образовать даже трёхгранного угла. Из углов правильных многоугольников, имеющих более 6 сторон, подавно нельзя образовать никакого выпуклого многогранного угла.
Отсюда следует, что гранями правильного многогранника могут служить лишь правильные треугольники, квадраты и правильные пятиугольники.
Таким образом, всего может существовать лишь пять видов правильных многогранников, указанных выше.
98. .Построение правильных многогранников. Изложенные выше рассуждения о возможных видах правильных многогранников доказывают, что может существовать не более пяти видов правильных многогранников.
Но из этих рассуждений еще не вытекает, что все эти пять видов правильных многогранников действительно существуют, т. е. что можно проведением плоскостей в пространстве осуществить построение каждого из этих пяти возможных правильных многогранников. Чтобы убедиться в существовании всех правильных многогранников, достаточно указать способ построения каждого из них.
Способ построения куба указать весьма легко. Действительно, берём произвольную плоскость P и в ней какой-либо квадрат; через стороны этого квадрата проводим плоскости, перпендикулярные к плоскости Р. Таких плоскостей будет четыре. Далее проводим плоскость Q, параллельную Р и отстоящую от неё на расстоянии, равном стороне квадрата. Шесть полученных плоскостей образуют грани куба; двенадцать прямых — пересечения каждой пары пересекающихся плоскостей — являются рёбрами куба, а восемь точек пересечения каждой тройки пересекающихся плоскостей служат вершинами куба. В этом легко убедиться, непосредственно рассматривая полученную совокупность точек, прямых и плоскостей. Умея построить куб, легко найти способ построения всех других правильных многогранников.
Построение правильного тетраэдра. Пусть дан куб (черт. 112).
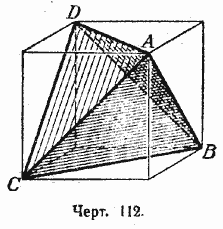
Возьмём какую-нибудь его вершину, например А. В ней сходятся три грани куба, имеющие форму квадратов. В каждом из этих квадратов берём вершину, противоположную точке А. Пусть это будут вершины куба В, С и D. Точки А, В, С и D служат вершинами правильного тетраэдра. Действительно, каждый из отрезков AB, ВС, CD, AD, BD и АС, очевидно, служит диагональю одной из граней куба. А потому вcе эти отрезки равны между собой. Отсюда следует, что в треугольной пирамиде с вершиной А и основанием ВСD все грани — правильные треугольники, следовательно, эта пирамида—правильный тетраэдр. Этот тетраэдр вписан в данный куб.
Полезно заметить, что оставшиеся четыре вершины куба служат вершинами второго правильного тетраэдра, равного первому и также вписанного в данный куб.
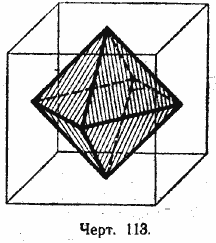
Построение октаэдра. Если в данном кубе построить центры всех его граней, то шесть полученных точек служат вершинами октаэдра. В этом легко убедиться, рассматривая чертёж 113.
Построение додекаэдра и икосаэдра. Если через каждое из 12 ребер куба провести плоскость, не имеющую с поверхностью куба других общих точек, кроме точек того ребра, через которое она проведена, то полученные 12 плоскостей образуют грани некоторого 12-гранника. Более подробное изучение формы этого многогранника показывает, что можно так подобрать наклон этих плоскостей к граням куба, что полученный 12-гранник будет додекаэдром.
Наконец, если мы умеем построить додекаэдр, то построение икосаэдра не представляет затруднений: центры граней додекаэдра служат вершинами икосаэдра.