ГЛАВА ЧЕТВЁРТАЯ
КРУГЛЫЕ ТЕЛА
Объём цилиндра и конуса
119. Определения. 1) За величину объёма цилиндра принимается предел, к которому стремится объём правильной призмы, вписанной в цилиндр, когда число боковых граней этой призмы неограниченно удваивается.
2) За величину объёма конуса (полного или усечённого) принимается предел, к которому стремится объём правильной пирамиды (полной или усечённой), когда число боковых граней пирамиды неограниченно удваивается.
120. Теоремы. 1) Объём цилиндра равен произведению площади основания на высоту.
2) Объём конуса равен произведению площади основания на треть высоты.
Впишем в цилиндр какую-нибудь правильную призму, а в конус— какую-нибудь правильную пирамиду; тогда, обозначив площадь основания призмы или пирамиды буквой В1, высоту их буквой Н и объём — V1 получим:
для призмы V1 = В1Н;
для пирамиды V1 = 1/3В1Н.
Вообразим теперь, что число боковых граней призмы и пирамиды неограниченно удваивается. Тогда В1 будет иметь пределом площадь В основания цилиндра или конуса, а высота Н остаётся без изменения; значит, произведения В1Н и 1/3 В1Н будут стремиться к пределам ВН и 1/3ВН, и потому объём V цилиндра или конуса будет:
для цилиндра V = ВН;
для конуса V = 1/3 ВН.
121. Следствие. Если радиус основания цилиндра или конуса обозначим через R, то В = πR2, поэтому
объём цилиндра V = πR2Н;
объём конуса V = 1/3 πR2Н.
122. Теорема. Объём усечённого конуса равен сумме объёмов трёх конусов, имеющих одинаковую высоту с усечённым конусом, а основаниями: один — нижнее основание этого конуса, другой — верхнее, третий— круг, площадь которого есть среднее геометрическое между площадями верхнего и нижнего оснований.
Теорему эту докажем совершенно так же, как раньше мы доказали теорему для объёма усечённой пирамиды (§ 92).
На верхнем основании усечённого конуса (черт. 134) поместим такой малый конус (с высотой h), который дополняет данный усечённый конус до полного.
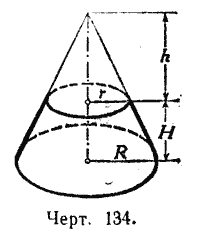
Тогда объём V усечённого конуса можно рассматривать как разность объёмов полного конуса и дополнительного. Поэтому
V = 1/3 πR2 (H + h) — 1/3 πr2h = 1/3 π [R2H + (R2— r2) h].
Из подобия треугольников находим: .
R/r = H+h/h
откуда получаем:
Rh = rH + rh; (R — r)h = rH; h = rH/R—r
Поэтому
V = 1/3 π [R2H + (R + r) rН] = 1/3 πH (R2 + Rr + r2) =1/3 πR2H + 1/3 πRrH + 1/3 πr2H
Так как πR2 выражает площадь нижнего основания, πr2 —площадь верхнего основания и πRr = √πR2 • πr2 есть среднее геометрическое между площадями верхнего и нижнего оснований, то полученная нами формула вполне подтверждает теорему.