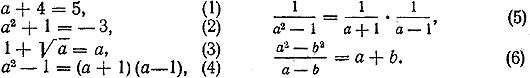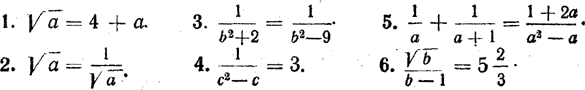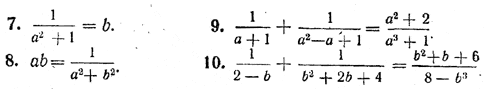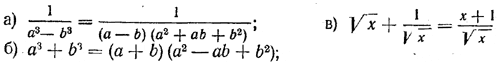|
|
ЛИНЕЙНЫЕ УРАВНЕНИЯ И НЕРАВЕНСТВА I Изучение алгебры и элементарных функций мы начинаем с рассмотрения линейных уравнений и неравенств. Эта тема знакома нам еще по курсу VIII класса. Прежде чем изучить ее более глубоко, вспомним некоторые уже известные нам понятия. § 1. Тождества. В математике часто приходится иметь дело с равенствами, то есть с такими записями, в которых два выражения соединены знаком = (знаком равенства). Прежде всего обратимся к числам. Если а и b — числа, то равенство а = b означает, что а и b — это просто одно и то же число. Наоборот, если а и b — разные числа, то пишут а =/= b. Например, 2 = 2, 2 + 3 = 5, 2 — 3 = — 1, но 7=/=6, 7 + 3=/= 0, 3 — 7 =/= 4. Труднее обстоит дело, когда равенство содержит какие-нибудь буквы, которыми обычно мы обозначаем неизвестные величины. Рассмотрим, например, такие равенства:
Каждая часть равенства (1) имеет смысл при любых значениях а. Это означает, что, какое бы числовое значение мы ни придали букве а, левая и правая части равенства (1) тоже примут некоторые числовые значения. Аналогичным свойством обладают также равенства (2) и (4). А вот с равенствами (3), (5) и (6) дело обстоит иначе. Правая часть равенства (3) определена при любых значениях а, а левая — лишь при неотрицательных значениях а. (Вспомните: извлекать квадратные корни можно лишь из положительных чисел и нуля.) Поэтому если равенство (3) рассматривать в целом, то следует сказать, что оно определено для всех неотрицательных значений а. Левая и правая части равенства (5) определены лишь при а =/= 1 и а =/= — 1. Если же а = 1 или а = — 1, то в знаменателях дробей получаются нули, а делить на нуль нельзя. Поэтому равенство (5) определено при всех значениях а, отличных от 1 и —1. Правая часть равенства (6) определена при любых значениях а и b, а левая лишь при а =/= b. Поэтому в целом равенство (6) имеет смысл для любых не равных друг другу чисел а и b. Значения букв, входящих в равенство, при которых имеют смысл и левая и правая части этого равенства, называются допустимыми значениями этих букв. Так, допустимыми значениями а в равенствах (1), (2) и (4) будут все числа, в равенстве (3) —все неотрицательные числа, в равенстве (5) —все числа, кроме 1 и — 1. В равенстве (6) допустимые значения а и b складываются из всевозможных пар не равных друг другу чисел. Если равенство содержит более одной буквы, то, говоря о допустимых значениях этих букв, мы должны иметь в виду одновременно каждую из этих букв. Например, можно сказать, что пары чисел (1,2) и (—5, 6) являются допустимыми, а пара (3,3) — не допустимой для букв а и b в равенстве (6). Однако не следует говорить, что значение 1 является допустимым для буквы а, так же как не следует говорить и то, что это значение не является допустимым для а. Ведь все зависит еще и от того, какое значение принимает при этом буква b. Если не только а, но и b равно 1, то равенство (6) теряет смысл; если же b =/= 1, то при а = 1 это равенство определено. Хотя в равенстве (1) допустимым является любое число, левая и правая части этого равенства принимают одинаковые числовые значения лишь при а = 1. При всех же остальных значениях а левая часть этого равенства принимает числовые значения, отличные от 5. Обе части равенства (2) не могут принять одинаковые числовые значения ни при каком значении а. Ведь выражение а2 + 1 принимает только положительные значения, а число — 3 является отрицательным. Прямо противоположным свойством обладает равенство (4). Какое бы значение мы ни придали букве а, левая и правая части этого равенства примут одинаковые числовые значения. О равенстве (5) этого сказать нельзя. При а = 1 и а = — 1 это равенство вообще теряет смысл, а в таком случае нельзя говорить о том, одинаковые или неодинаковые числовые значения принимают его отдельные части. Но числа 1 и — 1 не входят в область допустимых значений a. Поэтому можно сказать, что обе части равенства (5) принимают одинаковые числовые значения при любом допустимом значении а. Аналогично можно сказать и про равенство (6). Обе его части принимают одинаковые числовые значения при любых допустимых значениях а и b. Равенство, обе части которого принимают одинаковые числовые значения при любых допустимых значениях входящих в него букв, называется тождеством. К тождествам относятся, например, равенства (4), (5) и (6). Что же касается равенств (1), (2) и (3),. то их отнести к тождествам, очевидно, нельзя. Представляется вполне естественным потребовать, чтобы понятие тождества удовлетворяло следующему важному свойству, называемому свойством транзитивности. если равенства А = В и В = С являются тождествами, то и равенство А= С является тождеством. Можно, однако, показать, что введенное нами определение тождества этому требованию удовлетворяет не всегда Действительно, равенства | a | =(√a )2 (7) (√a )2 = а (8) в смысле нашего определения являются тождествами. Каждое из них имеет допустимыми значениями все неотрицательные значения а. Однако равенство | а | = а (9) имеет допустимыми значениями уже все значения а (положительные, отрицательные и нуль), а справедливо оно лишь для неотрицательных значений а. Следовательно, в смысле введенного нами определения равенство (9) не является тождеством. Выяснение того, когда такие неприятности могут возникнуть и когда они не возникают, выходит за пределы нашей программы и потому не может быть здесь проведено. Для избежания же этих неприятностей поступают таким образом. Вместо того чтобы говорить о тождествах как равенствах, справедливых для всех допустимых значений входящей в них буквы а, говорят о тождествах, имеющих место для какого-то заданного множества значений а. Тогда если равенства А = В и В = С являются тождествами на одном и том же множестве значений а, то для тех же значений а будет тождеством и равенство А = С. Упражнения Для каждого из данных равенств (№ 1—10) выяснить, при каких значениях входящих в них букв определены: а) левая часть равенства; б) правая часть равенства; в) равенство в целом.
11. Покажите, что равенство 2 — а = 3а — 4 не является тождеством. 12. Можно ли сказать, что равенства:
—выполняются при любых значениях входящих в них букв? Являются ли эти равенства тождествами? ОТВЕТЫ 1. Левая часть определена для любых неотрицательных чисел а, правая часть — для любых чисел а, равенство в целом — для всех неотрицательных чисел а. 4. Левая часть определена для всех чисел с, кроме 0 и 1, правая часть — для всех чисел с, равенство в целом—для всех чисел с, кроме 0 и 1. 5. Левая часть определена для всех а, кроме 0 и —1, правая часть — для всех чисел а, кроме 0 и 1, равенство в целом — для всех чисел а, кроме 0, —1 и 1. 6. Левая часть определена для всех неотрицательных чисел b, кроме 1, правая часть —для всех чисел b, равенство в целом — для всех неотрицательных чисел b, кроме 1. 8. Левая часть определена для всех пар (а, b), правая—для всех пар, кроме пары (0, 0), равенство в целом—для всех пар, кроме пары.(0, 0). |