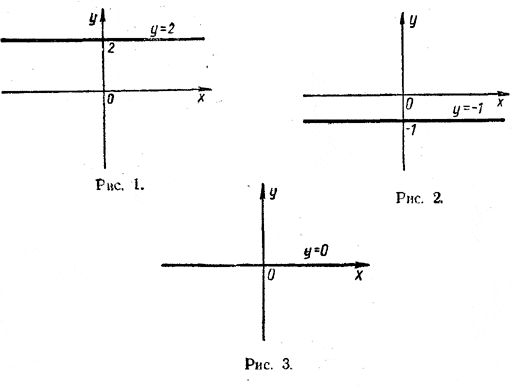
ЛИНЕЙНЫЕ УРАВНЕНИЯ И НЕРАВЕНСТВА  I

§ 3 Линейные функции и их графики

Рассмотрим равенство

у = 2х + 1.                    (1)

Каждому значению буквы х это равенство ставит в соответствие вполне определенное значение буквы у. Если, например, x = 0, то у = 2 • 0 + 1 = 1; если х = 10, то у = 2 • 10 + 1 = 21; при х = — ¹/₂  имеем у = 2 • (— ¹/₂ ) + 1= 0   и т. д.   Обратимся к  еще к одному равенству:

у = х ²                    (2)

Каждому значению х это равенство, как и равенство (1), ставит в соответствие вполне определенное значение у. Если, например, х = 2, то у = 4; при х = — 3 получаем у = 9 и т. д. Равенства (1) и (2) связывают между собой две величины х и у так, что каждому значению одной из них (х) ставится в соответствие вполне определенное значение другой величины (у).

Если каждому значению величины х соответствует вполне определенное значение величины у, то эта величина у называется функцией от х. Величина х при этом называется аргументом функции у.

Таким образом, формулы (1) и (2) определяют две различные функции аргумента х.

Функция аргумента х , имеющая вид

у = ах + b,          (3)

где а и b — некоторые заданные числа, называется линейной. Примером линейной функции может служить любая из функций:

у = х + 2                (а = 1, b = 2);       
у = — 10               (а = 0, b = — 10);
у = — 3х               (а = — 3, b = 0);  
у = 0                     (а = b = 0).            

Как   известно из   курса   VIII    класса, графиком функции у = ах + b является прямая линия. Поэтому-то данная функция  и  называется  линейной.

Напомним, как строится график линейной функции у = ах + b.

1.  График функции  у = b.        При a = 0 линейная функция у = ах + b имеет вид у = b. Ее графиком служит прямая, параллельная оси х и пересекающая ось у в точке с ординатой  b.   На рисунке 1 вы  видите   график    функции у = 2 (b > 0), а на рисунке 2— график функции у = — 1  (b < 0).

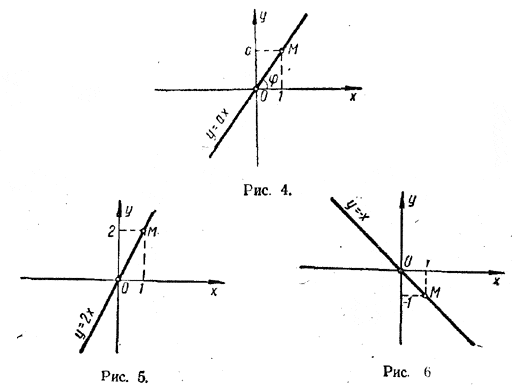
Если не только а, но и b равно нулю, то функция у= ах+ b имеет вид у = 0. В этом случае ее график совпадает с осью х (рис. 3.)

2.   График функции  у = ах.     При b = 0 линейная   функция у = ах + b имеет вид      у = ах.

Если а =/= 0, то графиком ее является прямая, проходящая через начало координат и наклоненная к оси х под углом φ, тангенс которого равен а (рис. 4). Для построения прямой у = ах достаточно найти какую-нибудь одну ее точку, отличную от начала координат. Полагая, например, в равенстве у = ах  х = 1, получим у = а. Следовательно, точка М с координатами (1; а) лежит на нашей прямой (рис. 4). Проводя теперь прямую через начало координат и точку М, получаем искомую прямую у = аx.

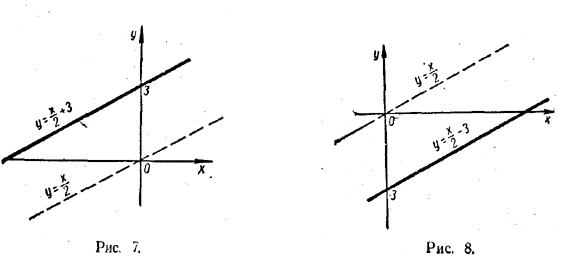
На рисунке 5 для примера начерчена прямая  у = 2х  (а > 0),   а на рисунке 6 — прямая у = — х (а < 0).

3. График  функции  у = ах + b.

Пусть b > 0. Тогда прямая у = ах + b получается посредством параллельного сдвига прямой у = ах на b единиц вверх. В качестве примера на рисунке 7 показано построение прямой у = ^x/₂ + 3.

Если b < 0, то прямая у = ах + b получается    посредством  параллельного сдвига прямой у = ах   на    — b единиц  вниз. В качестве примера   на рисунке 8 показано   построение   прямой   у = ^x/₂ — 3

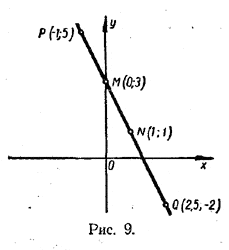
Прямую у = ах + b можно построить и другим способом.

Любая прямая полностью определяется двумя своими точками. Поэтому для построения графика функции у = ах + b достаточно найти какие-нибудь две его точки, а затем провести через них прямую линию. Поясним это на примере функции у = — 2х + 3.

 При х = 0 у = 3, а при х = 1 у = 1. Поэтому две точки: М с координатами (0; 3) и N с координатами (1;1) — лежат на нашей прямой. Отметив эти точки на плоскости координат и соединив их прямой линией (рис. 9), получим график функции у = — 2х + 3.

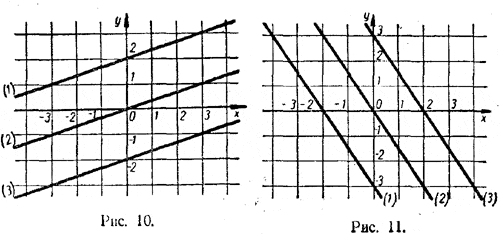
Вместо точек М и N можно было бы взять, конечно, и другие две точки. Например, в качестве значений х мы могли бы выбрать не 0 и 1, как выше, а — 1 и 2,5. Тогда для у мы получили бы соответственно значения 5 и — 2. Вместо точек М и N мы имели бы точки Р с координатами (— 1; 5) и Q с координатами (2,5; — 2). Эти две точки, так же как и точки М и N, полностью определяют искомую прямую у = — 2х + 3.

Упражнения

15. На одном и том же рисунке построить графики функций:

а) у = — 4;  б)  у = —2;   в)  у = 0;   г)  у = 2;   д) у  =  4.

Пересекаются ли эти графики с осями координат? Если пересекаются, то укажите координаты точек пересечения.

16.  На одном и томже рисунке построить графики функций:

а)  у = ^x/₄;   б) у =  ^x/₂;   в)  у = х;   г)  у = 2х ;    д)  у = 4х.

17.  На одном и том же рисунке построить графики функций:

а)  у = — ^x/₄;   б) у = —  ^x/₂;   в)  у = — х;   г)  у = — 2х ;    д)  у = — 4х.

Построить графики данных функций (№ 18—21) и определить координаты точек пересечения этих графиков с осями координат.

18.  у = 3+ х.            20.  у = — 4 — х.

19.  у = 2х — 2.       21. у = 0,5( 1 — 3х).

22.   Построить   график функции

у = 2x — 4;

используя этот график, выяснить: а) при каких значениях х    y = 0;

б) при каких значениях х значения у отрицательны и при каких — положительны;

в)   при каких значениях  х величины х и у имеют одинаковые знаки;

г) при каких значениях х величины х и у имеют разные знаки.

23.   Написать уравнения прямых, представленных на  рисунках 10 и 11.

24.   Какие из известных вам физических законов описываются с помощью линейных функций?

25.   Как построить график функции    у = — (ах + b),    если   задан   график   функции у = ах + b?