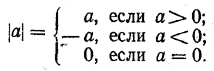ЛИНЕЙНЫЕ УРАВНЕНИЯ И НЕРАВЕНСТВА  I

§ 7 Уравнения, содержащие неизвестное под знаком абсолютной величины

Абсолютная величина числа а (обозначается | а |) определяется следующим образом:

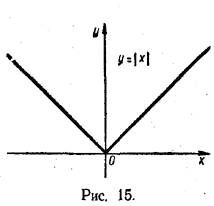
Например, |10| = 10;   — ¹/₃= | ¹/₃ |;   | — 100| =100 и т. д.

Каждому значению х соответствует вполне определенное значение | х |. Поэтому равенство у = | х | определяет у как некоторую функцию аргумента х. График этой функции приведен на рисунке 15.

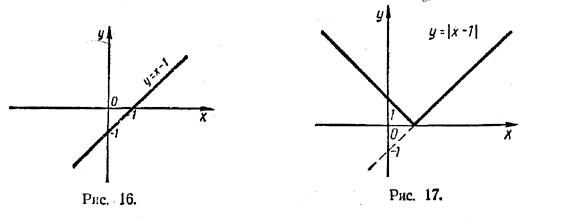
При x > 0 |x| = x, а при x < 0 |x |= — x; поэтому линия у = |x| при x > 0 совпадает с прямой у = х (биссектриса 1-го координатного угла), а при х < 0 — с прямой у = — х (биссектриса 2-го координатного угла).

Некоторые уравнения содержат неизвестное под знаком абсолютной величины. К таким относятся, например, уравнения |х — 1| = 2, |6 — 2х| = 3х + 1 и т. д. Решение их основано на том, что если абсолютная величина некоторого числа х   равна положительному числу а, то само это число х равно либо а, либо — а.  Так, если |х| = 10, то либо х =10, либо х = — 10.

Рассмотрим несколько примеров.

1.   Решить уравнение |х — 1|   = 2.

Разность х — 1 должна быть равна либо + 2, либо — 2. Если х — 1 = 2, то х = 3; если же х — 1 = — 2,  то  х = — 1. Проверка показывает, что оба эти значения удовлетворяют данному уравнению.

Ответ. Данное уравнение имеет два корня: x₁ = 3, x₂ = — 1.

2.  Решить уравнение | 6 — 2х| = 3х + 1.

Имеем: либо 6 — 2х = 3х + 1, либо 6 — 2х = — (3х + 1). В первом случае х = 1, а во втором х = — 7.

Проверка. При  х = 1     |6 — 2х| =  |4| = 4,     3x + 1 = 4; следовательно, х = 1 — корень данного уравнения.

При x = — 7   |6 — 2x| = |20| = 20, 3x + 1 = — 20; так как 20 =/= — 20, то х = — 7 не есть корень данного уравнения.

Ответ.    Данное   уравнение  имеет один корень: х = 1.

Подобные уравнения можно решать и графически. Решим, например, графически уравнение |х — 1| = 2. Для этого нужно прежде всего построить график функции у = |x — 1| . Это можно сделать  следующим образом. Сначала построим график функции у = х — 1 (рис. 16). Ту часть этого графика, которая лежит выше оси х, оставим без изменения. Для нее х — 1 > 0 и потому |х — 1| = х — 1.

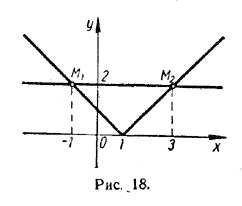
Ту же часть графика, которая лежит ниже оси х, отобразим симметрично относительно этой оси. Ведь для этой части х — 1 < 0 и потому |х — 1|=  — (х — 1). Полученная в результате линия (рис. 17 — сплошная линия) и будет графиком функции у  = |х—1|.

Эта линия пересекается с прямой у = 2 (рис. 18) в двух точках: M₁с абсциссой — 1 и  М₂ с абсциссой 3.

Поэтому уравнение |х — 1| = 2 имеет  два   корня:    х₁ = — 1,   х₂= 3.

Упражнения

Решить уравнения:

60.   1 — |х| = 0,5.

61.   1 + |х| = а.

62. | 1 — х| = 0,5.

63. |1 — х|  = а.

64. |х + 3|  = 3 + 2х.    

65. |7х— 1|= 21 —9х.

66.   |5 — х|  =  |х + 4|.

67.   |1 — 3х| = |3 — 2х| .

68. Покажите, что график функции у = |х — а| (а > 0) получается посредством параллельного сдвига графика функции у = |х|    на а единиц длины вправо.

Как строится график функции у = |х + а| (а > 0)?

69. Используя результат задачи 68, построить графики следующих функций;

а) у = |х — 2|;         б) у = |х + 3| .

70.   Как построить график функции у = |ах + b| , если задан график функции у = ах + b?

71. Может ли график функции у = ах + b совпасть с графиком функции у = |ах + b| ?

72.  Решить графически уравнения:

а) |2 + х|  = 3;    6) х =  |2 — х|;     в) |2х — 3|  = 3 — х.

73.  Исходя из геометрических соображений, выяснить, всегда ли имеют корни следующие уравнения:

а)   х = |ах + b|                  в) |ах + b| = с;

б)  |2х + b|   = 3;               г) |ах + b| = |сx + d| .

74.   Как построить график функции у = a|x| + b, если задан график функции у = ах + b?

ОТВЕТЫ