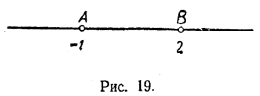
ЛИНЕЙНЫЕ УРАВНЕНИЯ И НЕРАВЕНСТВА  I

§ 8 Метод интервалов

При решении некоторых уравнений, содержащих неизвестное под знаком абсолютной величины, часто используют так называемый метод интервалов. Продемонстрируем этот метод на примере уравнения

|x + 1 |+ |x — 2| = 3.                (1)

Это уравнение содержит две абсолютные величины: | х + 1 | и | х — 2|. Первая из них обращается в нуль при х = — 1, а вторая — при х = 2. На числовой прямой отметим две точки: А с абсциссой — 1 и В с абсциссой 2 (рис. 19). Тем самым числовая прямая разобьется на три интервала.

Первый (бесконечный) интервал включает в себя все точки, лежащие левее А, Второй (конечный) интервал содержит в себе точки А и В, а также все точки, лежащие между ними. Третий (бесконечный) интервал состоит из всех точек, лежащих правее В. В любом из этих трех интервалов каждое из выражений  | х + 1 | и | х — 2| легко записывается без знака абсолютной величины. Так,

| х + 1 | =

 {

— х — 1 в первом интервале;
х + 1 во втором и в третьем интервалах.

Аналогично,

| х — 2| =

 {

— х +2 в первом  и во втором интервалах;
х — 1   в третьем интервале.

Поэтому левая  часть  уравнения  (1)  представляется  следующим образом:

в первом  интервале (— х — 1) + (— х +2) = — 2х + 1;
во втором интервале (х + 1) + ( — х + 2) = 3;
в третьем интервале (х + 1) + (х — 2) = 2х — 1.

Теперь нетрудно   найти все корни уравнения (1). Сразу же замечаем, что любое число из второго интервала

—  1 < х < 2

является корнем: ведь при любом значении х  из этого интервала левая и правая части уравнений (1) принимают одно и то же числовое значение 3.

Обратимся к первому интервалу. Если в нем имеются корни, то   они должны, очевидно, совпадать с корнями уравнения

— 2х + 1 = 3.

Это уравнение имеет единственный корень х = — 1, который мы уже получили раньше и  который, кстати, не попадает в первый интервал. (Значение х = —1 принадлежит второму интервалу.) Таким образом, в первом интервале уравнение (1) не имеет корней.

Аналогично можно установить, что уравнение (1) не имеет корней и в третьем интервале. Предлагаем учащимся убедиться в этом самостоятельно.

Итак, уравнение (1) имеет бесконечное множество корней. Каждое число, заключенное в интервале

—  1 < х < 2,

является его корнем. Никаких других корней это уравнение не имеет.

Упражнения

Решить уравнения:

75.  |х —1 |+ |х+ 1|= 2.               77. |х| + |х + 2| + |2 — х| = х + 1.

76. |5 — 2x|+ |х + 3| = 2 — 3х.     78. |1 — х| — |х + 3| = |х + 2|.

ОТВЕТЫ
Используются технологии uCoz