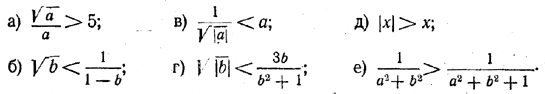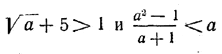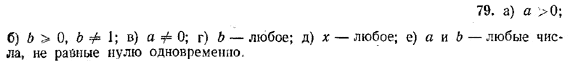|
|
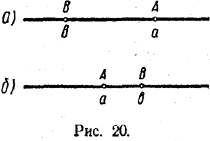
ЛИНЕЙНЫЕ УРАВНЕНИЯ И НЕРАВЕНСТВА I § 9 Неравенетва Если числа а и b равны между собой, то а — b = 0. Если же числа а и b не равны между собой, то разность а — b либо положительна, либо отрицательна. Если разность а — b положительна, то говорят, что число a больше числа b; записывается это таким образом: а > b. (1) Если разность а — b отрицательна, то говорят, что число а меньше числа b; записывается это таким образом: а < b. (2) Например, 5 > 3, поскольку разность 5 — 3 = 2 положительна; — 7 <. — 6, так как разность (— 7) — (— 6) = — 1 отрицательна. Записи (1) и (2) называются числовыми неравенствами, а знаки > и <, участвующие в них, —знаками неравенства. Числовые неравенства допускают простую геометрическую интерпретацию. Будем изображать числа точками числовой прямой. Пусть числу а соответствует точка А, а числу b — точка В. Тогда, если а > b, то точка А будет лежать правее точки В (рис. 20, а). Если же а < b, то точка А будет лежать левее точки В (рис. 20, б).
До сих пор мы говорили лишь о таких неравенствах, обе части которых представляют собой вполне определенные числа. (Правда, для общности рассуждений мы обозначали эти числа буквами.) Однако в математике часто приходится иметь дело и с такими неравенствами, отдельные члены которых, выраженные с помощью букв, могут принимать различные числовые значения, например, √a > а, (3) 1/a > 3, (4) а — 1 < а, (5) √a + √b < 0,5. (6) Допустимыми значениями букв, входящих в неравенство, называются такие значения этих букв, при которых обе части неравенства имеют смысл. Очевидно, что допустимыми значениями а в неравенстве (3) служат все положительные числа и нуль, в неравенстве (4) — все числа, кроме нуля, в неравенстве (5) — все числа. Для неравенства (6) допустимые значения а и b складываются из всевозможных пар неотрицательных чисел. Рассмотрим подробнее неравенст во (3). Оно, как мы уже говорили, определено для всех неотрицательных значений а. Однако не каждое из указанных чисел удовлетворяет этому неравенству. Действительно, при а = 0,25 √a = 0,5. Поскольку 0,5 > 0,25, то число а = 0,25 удовлетворяет неравенству (3). А вот число 4 ему уже не удовлетворяет, поскольку √4 <. 4. Таким образом, неравенству, содержащему букву, могут удовлетворять одни допустимые значения этой буквы и не удовлетворять другие допустимые значения этой буквы. Неравенство, которому удовлетворяют все допустимые значения входящих в него букв, называется тождественным неравенством. Примером такого неравенства может служить хотя бы неравенство (5). При любом значении а а — 1 < а. Неравенство (4) нельзя отнести к тождественным неравенствам; ему не удовлетворяет, например, значение а = 1: 1/1 < 3. Упражнения 79. Найти допустимые значения букв, входящих в неравенства:
80. Можно ли сказать, что неравенствам
удовлетворяют любые значения входящих в них букв? Являются ли эти неравенства тождественными? ОТВЕТЫ
|