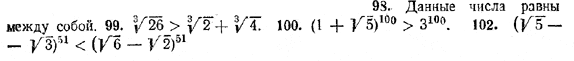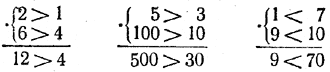
ЛИНЕЙНЫЕ УРАВНЕНИЯ И НЕРАВЕНСТВА  I

§ 12 Почленное умножение неравенств

Теорема. Неравенства одинакового смысла с положительными частями можно почленно умножать.

Доказательство. Пусть а > b и с > d, причем числа а, b, с и d положительны. Докажем, что aс > bd.

Умножив неравенство а > b почленно на положительное число с, получим ас > bc. Умножив затем неравенство с > d почленно на положительное число b, получим bc > bd. Теперь имеем: ас > bc, a bc > bd. Но тогда по второму основному свойству неравенств (§ 10) должно быть ас > bd.

Аналогично может быть рассмотрен случай, когда a < b и c < d.

Примеры:

Следствие 1. Если а > b, причем числа а и b положительны, то для любого натурального п

аⁿ  >  bⁿ.

Действительно, умножая почленно неравенство а > b само на себя,  получим а² > b². Умножая затем почленно полученное неравенство на исходное неравенство а > b, получим а³ > b³ и т. д.

Следствие 2. Если числа  а   и   b  положительны  и

аⁿ  >  bⁿ                (1)

(п — натуральное число), то а > b.

Действительно, возможен один из трех случаев: а = b, a < b и а > b.
Если    а = b,    то    аⁿ  =  bⁿ.
При а < b мы имели бы b > а, и потому по следствию 1  bⁿ > аⁿ . И то и другое противоречит неравенству (1).      
Остается признать, что а > b.

Пример.   Определить, какое число больше: √5  + √6  или  √3  + √8 .

Возвысим оба числа в квадрат:

(√5  + √6 )² = 5 + 2√30  + 6 = 11 + 2√30  ;
(√3  + √8 )² = 3 + 2√24  + 8 = 11 + 2√24

Квадрат первого числа больше квадрата второго числа. Так как эти числа положительны, то по следствию 2

√5  + √6  > √3  + √8 :

Упражнения

93.  Любые  ли  два   неравенства   одинакового  смысла   можно почленно умножить? (Рассмотрите пример:    3 > — 10   и    — 2 > — 7.)

94.   а) Всегда ли из а > b вытекает, что аⁿ  >  bⁿ ? Ответ   пояснить  примерами.

б) Следует ли из аⁿ  <  bⁿ, что а < b? Ответ пояснить примерами.

В задачах № 95—102 сравнить данные числа, то есть выяснить, какое из них больше и какое меньше:

95. √2  + √3  и  √7 .                                99*. ³√2 + ³√4  и ³√26?

96. √5  + √3   и  √6  + √2                    100. (1 + √5)¹⁰⁰ и 3¹⁰⁰.

97. √11 — √10  и √6  — √5 .              101. (√7 +√2)⁹ и 4⁹.

98. √8  — √15  и  ¹/₂(√30 — √2 )        102. (√5 —√3)⁵¹ и  (√6 —√2)⁵¹

ОТВЕТЫ