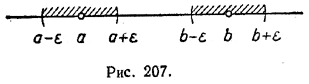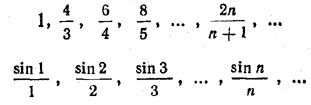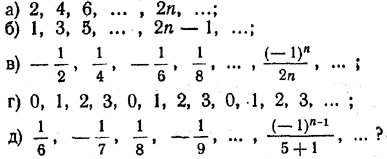ЧИСЛОВЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ  VI

§ 132 Сходящиеся и расходящиеся числовые последовательности

Теорема.  Числовая  последовательность не может иметь более одного предела.

Для доказательства предположим противное. Пусть некоторая числовая последовательность a₁, a₂,..., a_n, ... имеет несколько пределов. Допустим, что а и b — два таких предела. Для определенности будем считать, что а < b. Выберем положительное число ε так, чтобы отрезки (а — ε, а + ε) и (b — ε, b + ε) не  перекрывались друг другом* (рис. 207).

* В качестве такого ε  можно, например, взять

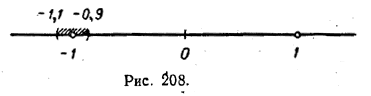
Тогда все числа нашей последовательности, начиная с некоторого, должны находиться, с одной стороны, в отрезке (а — ε, а + ε), а с другой — в отрезке (b — ε, b + ε). Но это невозможно, так как эти отрезки не перекрываются. Получено противоречие; значит, предположение о существовании двух различных пределов неверно.

Итак, любая числовая  последовательность может иметь не более одного предела. А каждая ли числовая последовательность имеет предел? Чтобы выяснить этот вопрос, рассмотрим последовательность

—1, 1, —1, 1, —1, 1, ...

с общим членом

a_n = (—1)ⁿ.

Каждый ее член, стоящий на нечетном месте, изобразится на числовой прямой точкой с абсциссой —1, а каждый член, стоящий на четном месте, — точкой с абсциссой 1. Уже отсюда ясно,  что если только эта последовательность имеет предел, то он равен либо —1, либо 1. Пусть, например, предел существует и равен —1. Тогда все члены последовательности, начиная с некоторого, должны укладываться, например, в интервале (—1—0,1; —1+0,1), или (—1,1; —0,9), что соответствует числу ε = 0,1 (рис. 208).

Но это не так, поскольку члены, равные 1, не попадают в  этот интервал.   Аналогично доказывается,    что и  1  не является пределом рассматриваемой последовательности.

Таким образо,м, последовательность —1; 1; —1; 1; ... не имеет предела.

Рассмотрим еще один пример — натуральный  ряд чисел 1, 2, 3, ..., п, ... .

Точки числовой прямой, соответствующие членам этой последовательности (рис. 209 ), не скапливаются ни у какой точки.

Какую бы   точку на числовой   прямой   мы   ни   взяли,   точки, соответствующие натуральному ряду чисел, рано  или поздно «перешагнут» через нее и уйдут как угодно далеко вправо. Следовательно, натуральный ряд чисел также не имеет предела.

Числовая последовательность, имеющая предел, называется сходящейся,  а не имеющая предела — расходящейся.

Например,  последовательности

(см. примеры 1 и 2, § 131) являются сходящимися, а последовательности

— 1, 1, —1, 1, —1, 1, ... ,

1, 2, 3, 4, ...

— расходящимися.

Упражнение

951. Какие из данных последовательностей являются сходящимися и какие расходящимися: