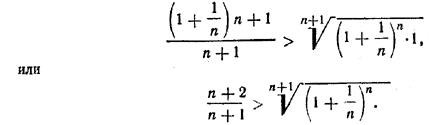|
|
ЧИСЛОВЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ VI § 134. Число е Рассмотрим бесконечную числовую последовательность (1+ 1/1 ), (1+ 1/2 )2, (1+ 1/3 )3,... (1) с общим членом an = (1+ 1/n )n Покажем, что эта последовательность является монотонно возрастающей и ограниченной. 1) Применим теорему о среднем арифметическом и среднем геометрическом (см. гл. I, § 16) к п + 1 числу: (1+ 1/n ), (1+ 1/n ), ... , (1+ 1/n ), 1; получим
Возводя обе части последнего неравенства в (п + 1)-ю степень, получаем
или an+1 > an Тем самым доказано, что рассматриваемая последовательность является монотонно возрастающей. 2) Теперь докажем, что наша последовательность является ограниченной Для этого рассмотрим еще одну последовательность: (1— 1/1 ), (1— 1/2 )2, (1— 1/3 )3,... (2) с общим членом bn = (1— 1/n )n Аналогично тому, как мы доказали монотонность последовательности (1), может быть доказана и монотонность последовательности (2): bn+1 > bn Далее,
Поэтому для всех п > 1 an = 1/bn Так как последовательность (2) монотонно возрастает, все ее члены, начиная с третьего, больше второго члена. Поэтому для всех п > 3 bn > b2 = (1— 1/2 )2 = 1/4 Следовательно, для всех п > 3 an < 1/b2 < 4. Это неравенство верно и при п = 1 и п = 2, так что для всех натуральных п 0< (1+ 1/n )n < 4. Тем самым доказана ограниченность последовательности (1). Теперь на основании теоремы о пределе монотонной ограниченной последовательности можно заключить, что предел последовательности (1) существует. Этот предел принято обозначать буквой е:
Подсчитано, что е = 2,7182818284... . Иногда для запоминания того или иного числа цифры этого числа связывают с какой-нибудь знаменательной датой. Легко, например, запомнить первые девять знаков числа е после запятой, если обратить внимание на то, что 1828 — это год рождения Льва Толстого! Число е является иррациональным. Более того, как показал французский математик Э р м и т (1822—1901), это число не может быть корнем никакого алгебраического уравнения с целыми коэффициентами. Такие иррациональные числа называются трансцендентными (см. гл. II). Предел (3) является одним из тех замечательных пределов, которые лежат в основе многих математических исследований. Число е играет особую роль в математике. Однако, если бы мы захотели убедиться в этом, нам пришлось бы заняться уже высшей математикой. |