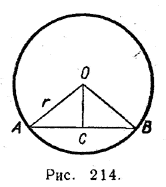
ЧИСЛОВЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ  VI

§ 141  Площадь круга.

Пусть s₄ ,  s₈ ,  s₁₆ , ... , , ...— последовательность площадей правильных 4-, 8-, 16-угольников и т. д., вписанных в окружность радиуса r.

Легко показать, что последовательность эта монотонно возрастает,   ограничена   и, следовательно, имеет предел

s = 

Можно доказать, что такой же предел имеет последовательность s₃ ,  s₄ ,  s₅ , ... ,s_n, ... площадей правильных 3-, 4-, 5-угольников и т. д., вписанных в ту же самую окружность. Этот предел по определению и принимается за площадь круга радиуса r.

Теперь выведем формулу для нахождения площади круга по его радиусу r. Пусть АВ — сторона правильного п-угольника (рис. 214), вписанного в окружность радиуса r, p_n — периметр этого многоугольника, a s_n— его площадь.

Имеем:

s_n = n • s_/\ OAB = n • ¹/₂ АВ • ОС,

но п • АВ = p_n.  Поэтому

s_n = ¹/₂  p_n • ОС.                                    (1)

Покажем, что при п —> ∞ ОС неограниченно приближается к r. Действительно   (рис.   214),

r — ОС = ОА— ОС.

Из треугольника АОС получаем:

0 < ОА — ОС < АС = ¹/₂ АВ

(разность двух сторон треугольника меньше третьей .стороны).

Поэтому r — ОС < ¹/₂ АВ.   Но АВ = ,     p_n < 2πr. Следовательно,

0 < r — ОС<. ¹/₂ • 2π ^r/_n = ^πr/_n.   При  возрастании  п дробь ^πr/_n становится сколь угодно малой. Поэтому | ОС — r | при п —> ∞ становится и остается меньше любого наперед заданного положительного числа ε:

| ОС — r | < ε.

А это и означает, что предел ОС при  п —> ∞ равен r. Теперь из  равенства  (1)  получаем:

s =  s_n =   (¹/₂  p_n  • ОС) = ¹/₂  (p_n  • ОС) = ¹/₂  p_n • ОС =

= ¹/₂ • 2πr • r  = πr².

Итак,

s = πr²

Площадь круга радиуса r равна произведению числа π на квадрат радиуса этого круга.

Упражнение

963. Какое определение вы предложили бы для площади, ограниченной произвольной замкнутой линией (см.,   например,   рис. 215)?