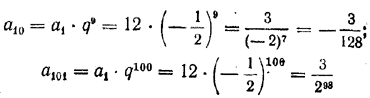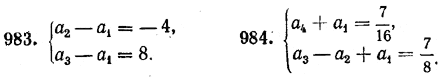ЧИСЛОВЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ  VI

§ 145. Геометрическая прогрессия.
Формула общего члена геометрической прогрессии

Геометрической прогрессией называется такая числовая последовательность, каждый член которой, начиная со второго, равен предыдущему, умноженному на некоторое постоянное для данной последовательности число, отличное от нуля.

Примеры геометрической прогрессии:

1,   ¹/₃ ,    ¹/₉ , ¹/₂₇ , ... ,

2,   8,   32,   128  , ...  ,

12, — 6, 3, — ³/₂,  .....,

¹/₅ ,  —  ²/₅ , ⁴/₅ ,  — ⁸/₅ , ... .

В каждой из этих последовательностей любой член, начиная со второго, получается из предыдущего путем умножения в первом случае на ¹/₃, во втором — на 4, в третьем — на ( — ¹/₂ ) , в четвертом — на   (—2).

Геометрическую прогрессию, очевидно, можно определить и таким образом:

числовая последовательность a₁ , a₂ , a₃ ,... , a_n, ...  называется геометрической прогрессией, если для любого п

a_n+1 = a_n• q,

где  q — некоторое постоянное для данной последовательности и отличное от нуля число.

Это число q называется знаменателем геометрической прогрессии.

Для приведенных выше примеров q равно в первом  случае ¹/₃ , во втором 4, в третьем— ¹/₂ , в четвертом — 2.

Геометрическая   прогрессия   называется   возрастающей,   если | q  |> 1, и убывающей, если | q | < 1. Так, из приведенных выше геометрических прогрессий первая (q = ¹/₃) и третья (q = — ¹/₂ ) — убывающие, а вторая (q = 4) и четвертая (q = —2) — возрастающие.

Пусть знаменатель  геометрической прогрессии a₁ , a₂ , a₃ ,...  равен q. Тогда по определению

a₂ = a₁ • q,

a₃ = a₂ • q = (a₁ • q) • q =  a₁ • q²

a₄ = a₃ • q = (a₁ • q²) • q =  a₁ • q³

и т. д.  Очевидно, что при любом п > 1

a_n = a₁ • q ^n—1             (1)

то есть п-й член геометрической прогрессии, равен произведению ее первого члена на знаменатель прогрессии в степени п— 1.

Формула   (1)  называется формулой  общего члена геометрической  прогрессии.

Например, для  геометрической  прогрессии

12, — 6, 3, — ³/₂,  ...

a₁ = 12, q = — ¹/₂ .

Поэтому

и  т.  д.

981. Написать формулу общего члена геометрической прогрессии,  в  которой:

а)  a₁ = 2, a₂ = ¹/₂;               д) a₁ = sin φ, a₂ = 2 sin φ;

б)  a₁ = 3, a₄ = — ¹/₃;         е) a₁ = tg φ,  a₂ = ¹/₂ tg φ;

в) a₃ = a₅ = —1;                ж) a₁ = tg φ, a₂ = 1;

г) a₄ = —54,  a₅ = 162;      з) a₁ = 1,   a₄ = 8.

982.  Получить формулу  общего члена  геометрической  прогрессии  путем почленного умножения равенств:

a₂ = a₁ • q
a₃ = a₂ • q
.......................
a_n = a_n—1 • q

(Сравните с арифметической  прогрессией,  §  142.)

Составить геометрические прогрессии по следующим данным (№  983—984):

985.   Найти  формулу,   выражающую  произведение  п   первых членов геометрической прогрессии через ее первый член и знаменатель.

986.   Если все члены геометрической   прогрессии  умножить на соответствующие (по номеру занимаемого места) члены другой геометрической прогрессии, то будет  ли полученная последовательность  геометрической прогрессией?

987. Две   геометрические    прогрессии     почленно     сложили. В каком случае полученная последовательность будет геометрической   прогрессией?

988.    Доказать,   что   в   конечной   геометрической   прогрессии произведение   членов,   равноудаленных от концов,  равно произведению   крайних   членов.

ОТВЕТЫ