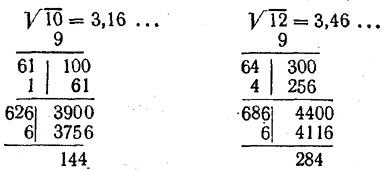
ЛИНЕЙНЫЕ УРАВНЕНИЯ И НЕРАВЕНСТВА  I

§ 19 Приближенное сложение и умножение на число

Пусть а' есть приближенное значение числа а с точностью до ε₁ и а b' — приближенное значение числа b с точностью до ε₂. Тогда сумма а' + b' будет приближенным значением числа а + b. Какова же точность такого приближения? Чтобы выяснить этот вопрос, воспользуемся свойством абсолютной величины суммы. Имеем:

|(а + b) — (а' + b')| = |(а — а') + (b — b') |< | а — а' | + | b—b'|.

По условию |а — a'| < ε₁ , а |b — b'|   < ε_{2 .}  Следовательно,

|(а + b) — (а' + b')|  <  ε₁ + ε₂

Но в тако,м случае можно сказать, что а + b ≈ а' + b' с точностью до ε₁ + ε_{2 .} Итак, мы доказали теорему.

Теорема 1. Если а  ≈ а'  с точностью до ε₁  , а b ≈  b'  с точностью до ε₂, то  а + b ≈ а' + b'  с точностью до ε₁ + ε₂.

Примеры. 1) С какой точностью можно найти сумму двух чисел, если одно из них известно с точностью до 0,1, а другое — с точностью до 0,2?

Теорема 1 в данном случае гарантирует точность 0,1 + 0,2 = 0,3.

2) Сумму √10 + √12 нужно найти с точностью до 0,1. Будем извлекать корни из 10 и 12 по известному алгоритму:

Двух десятичных знаков вполне достаточно. В этом случае каждое из слагаемых мы находим с точностью до 0,01. Поэтому по теореме  1  сумма √10 + √12 ≈ 3,16+3,46=6,62 будет   найдена с точностью до 0,01 + 0,01 = 0,02 < 0,1. Согласно требованию задачи окончательно запишем: √10 + √12 ≈ 6,6. Ограничиться при извлечении корней лишь одним десятичным знаком было бы нехорошо. В этом случае мы нашли бы приближенные значения слагаемых с точностью до 0,1. Но тогда у нас не было бы уверенности в том, что сумма √10 + √12 ≈ 3,1 + 3,4 = 6,5 будет найдена с точностью до 0,1. Ведь теорема 1 гарантировала бы лишь точность 0,1 +0,1 = 0,2, которая нас не устраивает.

Теорема 2. Если а' — приближенное значение числа а с точностью до ε, то ka' есть приближенное значение числа ka с точностью до |k|ε.

Например, с точностью до  0,1  √10 ≈ 3,1. Поэтому 5√10 ≈  5 • 3,1 = 15,5 с точностью до 5 • 0,1 = 0,5. Аналогично  —7√10 ≈ — 7 • 3,1 = — 21,7   с   точностью   до |— 7| • 0,1 = 7 • 0,1 = 0,7.

Доказательство теоремы 2. Если а' есть приближенное значение а с точностью до ε, то |а — а'|< ε . Поэтому |ka — ka'| = |k(a — а')| = |k| •  |а — а'| < |k |• ε. что и требовалось доказать.

В  заключение рассмотрим следующий  пример.  

Пусть с точностью до 0,1    a ≈ а' = 2,7;    b ≈ b' = 3,6.    Требуется найти приближенное    значение выражения 5а — 3b и определить точность этого приближения. Имеем:

5а — 3b ≈ 5а' — 3b' = 5 • 2,7 — 3  • 3,6 = 13,5 — 10,8 = 2,7.

Точность этого результата можно оценить, используя свойство абсолютной, величины суммы:

|(5а — 3b)  —  (5а' — 3b' )| = | (5а—5а') — (3b — 3b') | < |5а—5а'|  + |3b — 3b'| = 
= | 5(а — а')| + | 3(b — b') | = 5|а — а'|+3|b — b'| < 5 • 0,1 + 3 • 0,1   = 0,8.

Итак, 5а — 3b ≈  2,7 с точностью до 0,8.

Упражнения

149.  Вычислить с точностью до 0,1:

а) √2+√17;       б) √12 + ²/₇;         в)5√3;        г) ³⁶⁷/₅₄₆ — ¹/₇₅

150.   Известно, что с точностью до 0,01   a ≈ —3,05; b ≈ 3,01. Найти приближенные значения выражений:

а) 2а + 7b;   б) 3а — 5b;   в) —а — 4b.

Определить точность полученных приближений.

151.   Числа а и b заданы с одинаковой точностью ε. Каким должно быть ε, чтобы с точностью до 0,001 можно было бы найти:

а) а + b;    б) а — b;    в) а — 10b?

ОТВЕТЫ

149. а) 5,5; б) 3,7; в) 8,6; г) 0,6.   150. а) 14,97 с точностью до 0,09; б) —24,20 с точностью до 0,08; в) —8,99 с точностью до 0,05.   151.   а) 0,0005;   б) 0,0005; в) 0,00009 (точнее, ¹/_{1 1000}) .