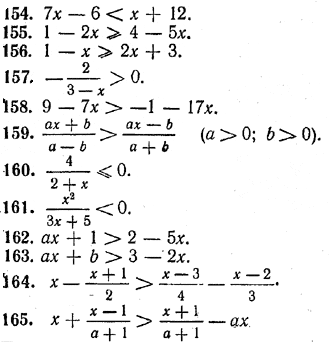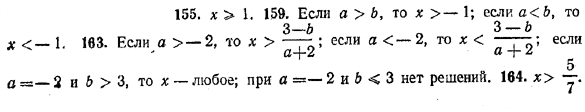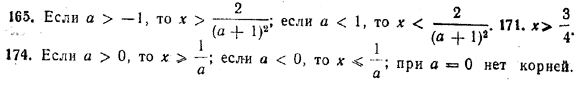ЛИНЕЙНЫЕ УРАВНЕНИЯ И НЕРАВЕНСТВА  I

§ 21 Линейные неравенства.

Так называются неравенства, левая и правая части которых представляют собой линейные функции относительно неизвестной.величины.  К ним относятся, например, неравенства

2х — 1 > — х + 3;       7х < 0;

5 > 4 — 6х;                   9 — х < х + 5

и т. д. Для определенности мы рассмотрим лишь неравенства, содержащие знак >. Линейное неравенство, содержащее знак >, имеет вид:

ах + b > сх + d.                            (1)

Если в неравенстве (1) а =/= с, то такое неравенство называется также неравенством 1-й степени. Очевидно, что всякое неравенство 1-й степени является вместе с тем и линейным неравенством.   Обратное утверждение неверно.   Например,   неравенство 0 • х > — 2 является линейным, но не является неравенством 1-й степени.

Перенося сх из правой части неравенства (1) в левую, а b из левой  части  в   правую,   получим:

(а — с) х > d — b.

Таким образом, любое линейное неравенстве сводится к эквивалентному неравенству вида

тх > п,                              (2)

где m  и  n — некоторые заданные числа, а  х — неизвестная величина.

Если m > 0, то, деля обе части неравенства (2) на т,   получим х > ⁿ/_m. Это соотношение и определяет множество всех тех значений величины х, при которых выполняется неравенство (2). Геометрически это множество   изображается в   виде   той   части числовой прямой, которая лежит справа  от  точки   с   абсциссой ⁿ/_m  (рис. 23).   Сама  точка —   в   это множество   не    включается. На рисунке это    отмечено   стрелочкой,    обращенной    к  точке с  абсциссой   ⁿ/_m.

Если т < 0, то, деля обе части неравенства (2) на т и меняя при этом знак неравенства на противоположный, получаем

х < ⁿ/_m

Это соотношение определяет множество всех тех значений величины х, при которых в данном случае выполняется неравенство (2). Геометрически это множество изображается в виде той части  числовой прямой, которая расположена слева от точки с  абсциссой   ⁿ/_m  (рис. 24). Сама точка х = ⁿ/_m в это множество не включается.  На рисунке это отмечено стрелочкой,  обращенной к точке с абсциссой ⁿ/_m .

Теперь предположим, что т = 0. Тогда неравенство (2) принимает вид:

0 • х  > п.

Если число п  отрицательное, то это неравенство выполняется при всех значениях х. В противном же случае оно не имеет  решений.

Мы рассмотрели линейные неравенства, содержащие знак >. Неравенства, содержащие знаки >, < и < , решаются аналогично.   Рассмотрим   несколько   примеров.

1.   Решить неравенство

х + 4 > —2х + 3.

Перенося —2х в левую, а 4 в правую часть, получаем 3х > —1, откуда х > —¹/₃.

На числовой прямой (рис. 25) отмечены  все те значения х, которые  удовлетворяют данному неравенству.

2.   Решить неравенство

3 — 7х > х — 5.

Перенося х в левую, а 3 в правую часть, получим —8х > — 8. Разделим обе части этого неравенства на —8. Поскольку это число отрицательно, то знак неравенства при этом нужно изменить на противоположный. В результате получим х < 1. Множество всех таких значений х отмечено на рисунке 26 (точка х = 1 включается в это множество).

Упражнения

Решить данные неравенства (№ 154—165) и отметить полученные результаты на числовой прямой:

При   каких  значениях  х    определены    данные      выражения (№ 166 -169).

166. √7 + 3х       168.  √2х + 4

167.  √5 — х     169.    √1 — 2х  +  √х

170. Может ли неравенство  а²х < а + 1   не  иметь   решений?

Решить   уравнения:

171.    |4x — 3|= 4x — 3.            173. |6x — а| = а — 6x.

172.    |7 — 2x| = 2x — 7.          174.  | ах — 1| = ах — 1.

ОТВЕТЫ