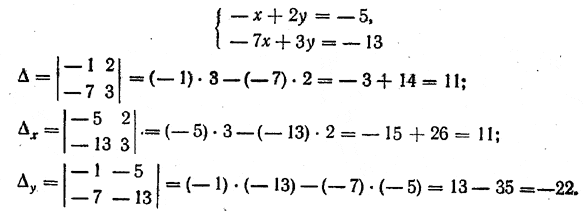ЛИНЕЙНЫЕ УРАВНЕНИЯ И НЕРАВЕНСТВА  I

§29 Главный и вспомогательный определители системы двух линейных ypaвнений с двумя неизвестными.

Главным определителем системы уравнений

         (1)

называется определитель

составленный из коэффициентов при неизвестных х и у. Этот определитель мы будем обозначать греческой буквой Δ (дельта). Очевидно, что

Δ= a₁b₂ — a₂b₁

Первым вспомогательным определителем системы уравнений (1) называется определитель

Он получается из главного определителя этой  системы уравнений путем замены первого столбца на столбец свободных членов.   Этот определитель мы будем обозначать   Δ_x. Индекс (то есть значок) х при Δ указывает,   что в главном определителе Δ первый столбец, составленный из коэффициентов при х в системе уравнений (1), заменен на столбец свободных членов . Очевидно, что

Δ_x = c₁b₂ — c₂b₁

Вторым вспомогательным определителем системы уравнений (1) называется определитель

'

который получается из главного определителя этой системы путем замены второго столбца на столбец свободных членов. Этот определитель мы будем обозначать  Δ_y. Очевидно,  что

Δ_y = a₁c₂ — a₂c₁.

Пример. Для системы уравнений

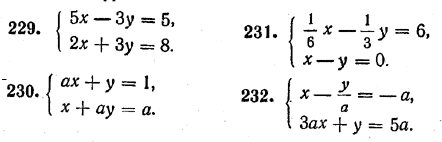
Вопрос о том, какую пользу приносят введенные нами определители Δ , Δ_x и Δ_y при решении системы уравнений (1), мы выясним в следующих параграфах.

Упражнения

Найти  главный и вспомогательные определители для следующих систем уравнений:

ОТВЕТЫ

231. ¹/₆; —6;—6.    232. 4;   5 — а;   5а+ 3а² (а =/= 0).
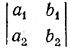
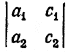