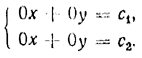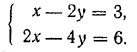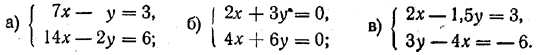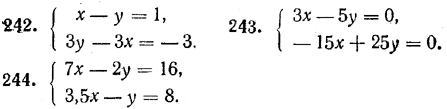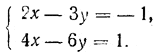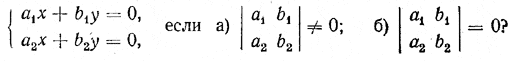|
|
ЛИНЕЙНЫЕ УРАВНЕНИЯ И НЕРАВЕНСТВА I § 32. Случай, когда и главный и оба вспомогательных определителя системы уравнений равны нулю В предыдущих параграфах, изучая систему уравнений
мы рассмотрели два случая: 1) случай, когда коэффициенты при неизвестных х и у не являются соответственно пропорциональными (Δ =/= 0); 2) случай, когда коэффициенты при неизвестных х и у соответственно пропорциональны, а коэффициенты при каком-нибудь неизвестном и свободные члены не являются соответственно пропорциональными (Δ = 0, а хотя бы один из определителей Δx и Δy отличен от нуля). Осталось рассмотреть еще один случай, когда и коэффициенты при неизвестных х и у и свободные члены соответственно пропорциональны, то есть a1 = ka2 , b1 = kb2, c1 = kc2 или a2 = k'a1 , b2 = k'b1, c2 = k'c1 Для определенности мы рассмотрим первый из этих двух вариантов. Система уравнений (1) в этом случае имеет вид:
Очевидно, что каждая пара чисел (x0 , y0), удовлетворяющая второму уравнению системы (2), должна удовлетворять и первому уравнению этой системы. Поэтому, для того чтобы решить систему уравнений (2), достаточно решить одно лишь второе уравнение этой системы. Другими словами, достаточно найти все такие пары чисел (x0 , y0), которые обращают уравнение a2 х + b2 у = c2 в числовое равенство. Предположим, что в этом уравнении хотя бы один из коэффициентов a2 и b2 отличен от нуля. Пусть, например, b2 =/= 0. Тогда в качестве x0 можно выбрать любое число t; y0 в этом случае найдется из условия a2 t + b2 y0= c2 , откуда Итак, в рассматриваемом случае система уравнений (2) имеет бесконечное множество решений. Все они задаются формулами
где t — любое число. Этот результат мы получили в предположении, что хотя бы один из коэффициентов a2 и b2 отличен от нуля. А если оба они равны нулю? Тогда система уравнений (2) имеет вид:
Такая система не представляет особого интереса. Если c1 = c2 = 0, то решением ее является любая пара чисел (x0 , y0). Если же хотя бы одно из чисел c1 и c2 отлично от нуля, то система (3) несовместна. Очевидно, что случай, когда a2 = b2 = 0, будет автоматически исключен, если дополнительно потребовать, чтобы среди коэффициентов при неизвестных x и у в системе уравнений (1) был хотя бы один отличный от нуля коэффициент. Мы доказали следующую теорему. Если коэффициенты при неизвестных и свободные члены в системе уравнений (1) соответственно пропорциональны и среди коэффициентов при неизвестных есть хотя бы один коэффициент, отличный от нуля, то система уравнений (1) имеет бесконечное множество решений. Все они получаются как решения одного того уравнения, которое содержит отличный от нуля коэффициент при неизвестном. Пример. Решить систему уравнений
Коэффициенты при неизвестных и свободные члены этой системы уравнений соответственно пропорциональны. Поэтому все решения этой системы уравнений можно получить как решения одного лишь первого уравнения х—2у = 3. Полагая х = t, находим, чтo у = 1/2 (t— 3). Итак, данная система уравнений имеет бесконечное множество решений: х = t, у = 1/2 (t— 3), где t — любое число. В частности, при t = 0 получается решение х = 0, у = — 3/2, при t = 5 — решение х = 5, у = 1 и т. д. Доказанную выше теорему полезно сформулировать и в терминах определителей. Если коэффициенты при неизвестных и свободные члены системы уравнений (1) соответственно пропорциональны, то, как легко получить непосредственно, используя (2), Δ = Δx = Δy = 0. Можно доказать и обратное утверждение. Если Δ = Δx = Δy = 0 и хотя бы один из коэффициентов при неизвестных системы уравнений (1) отличен от нуля, то коэффициенты при неизвестных и свободные члены такой системы уравнений будут соответственно пропорциональными. На доказательстве этого факта мы останавливаться не будем, хотя в принципе это и можно было бы сделать. Но, приняв его на веру, мы можем теперь доказанную выше теорему сформулировать следующим образом. Если и главный и оба вспомогательных определителя системы уравнений (1) равны нулю и среди коэффициентов при неизвестных есть хотя бы один отличный от нуля коэффициент, то система уравнений (1) имеет бесконечное множество решений. Все они получаются как решения одного того уравнения, которое содержит отличный от нуля коэффициент при неизвестном. Упражнения 241. (У с т н о.) Показать, что каждая из данных систем уравнений имеет бесконечное множество решений:
Решить системы уравнений (№ 242—244):
245. Дана система уравнений
а) Сколько решений имеет каждое уравнение этой системы? б) Сколько решений имеет система? 246. Сколько различных решений имеет однородная система уравнений
ОТВЕТЫ
|
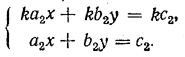 (2)
(2)