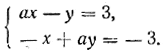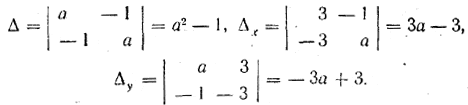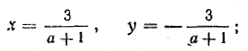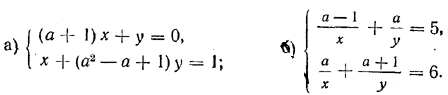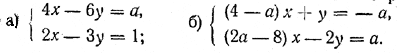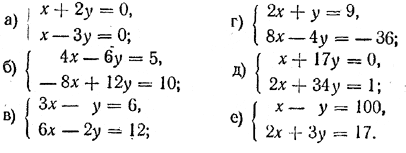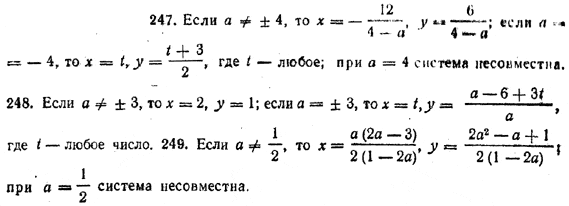ЛИНЕЙНЫЕ УРАВНЕНИЯ И НЕРАВЕНСТВА  I

§ 33 Таблица основных результатов о системе двух линейных уравнений с двумя неизвестными

Все результаты о системе уравнений

которые получены в § 30—32, приводятся в следующей таблице:

Пример.   Решить систему уравнений

Для этой системы

Пусть а²— 1 =/= 0, то есть а =/= — 1 и а =/= 1. Тогда Δ =/= 0 (случай 1), и потому система имеет единственное  решение:

Если а = — 1, то Δ = 0, Δ_x = — 6, Δ_y = 6. В этом случае система будет несовместной (случай 2).

Если же а = 1, то Δ  = Δ_x = Δ_y = 0 (случай 3). В этом случае система будет иметь бесконечное множество решений, причем все они получаются в результате решения одного лишь первого (второго) уравнения.

При а = 1 первое уравнение обращается в х — у =3. Все решения этого уравнения можно записать в виде х = t,   у = t — 3, где t — любое число.

Итак, к задаче можно дать следующий ответ: если а =/= 1  и  а =/=  — 1, то данная система уравнений имеет единственное решение:

если а = — 1, то система несовместна; при а = 1 система имеет бесконечное множество решений, которые можно записать в виде

х = t,     у = t — 3,    где t — любое число.

Метод решения системы двух линейных уравнений с двумя неизвестными, с которым мы познакомились в этой главе, основан на использовании определителей 2-го порядка. В курсе высшей алгебры вводится понятие определителя порядка п для. любого натурального п и излагается метод решения системы п линейных уравнений, с п неизвестными с помощью таких определителей.  Этот метод очень важен как при решении теоретических вопросов, так и при исследовании систем уравнений с буквенными коэффициентами. Он широко применяется (как и само понятие определителя) не только в высшей алгебре, но и в других разделах высшей математики,  в  механике,   в  теоретической  физике.

Однако для практического решения систем линейных уравнений с чиcловыми коэффициентами самым экономным (в смысле объема производимых вычислений) оказывается известный вам по курсу VIII класса метод последовательного исключения неизвестных. Именно им пользуются всегда на практике.

Упражнения

Решить системы уравнений (№ 247—249):

250.  Доказать,  что каждая  из данных систем  уравнений не может иметь бесконечно много различных решений:

251.  Доказать, что каждая из данных систем уравнений либо несовместна, либо' имеет бесконечное множество решений:

252.   (У с т н о.)    Выяснить,   сколько  решений  имеет  каждая из данных систем уравнений:

ОТВЕТЫ