|
|
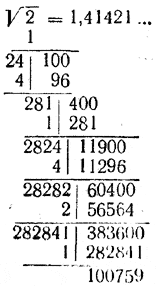
ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА II § 39 Извлечение квадратных корней из рациональных чисел Как мы знаем, в множестве рациональных чисел всегда выполнимо действие умножения. В частности, определено произведение m/n • m/n. Это произведение, как известно, называется квадратом числа m/n и обозначается (m/n)2 : (m/n)2 = m/n • m/n Таким образом, если некоторое число является рациональным, то квадрат его еcть также рациональное число. Это число, очевидно, положительно. А теперь поставим обратную задачу: всякое ли положительное рациональное число является квадратом некоторого рационального числа? На языке алгебраических уравнений эта задача может быть сформулирована следующим образом. Дано уравнение х2 = а, где а — некоторое положительное рациональное число, а х — неизвестная величина. Спрашивается: всегда ли это уравнение имеет р а ц и о н а л ь н ы е корни? Ответ на этот вопрос оказывается отрицательным. Рациональное число а можно выбрать так, что уравнение х2 = а не будет иметь ни одного рационального корня. В этом нас убеждает, в частности, следующая теорема. Теорема. Не существует рационального числа, квадрат которого равен 2. Доказательство будем проводить методом от противного. Предположим, что существует рациональное число m/n , квадрат которого равен 2: (m/n)2 = 2. Если целые числа т и п имеют одинаковые множители, то дробь m/n можно сократить. Поэтому с самого начала мы вправе предположить, что дробь m/n несократима. Из условия (m/n)2 = 2 вытекает, что т2 = 2п2 . . Поскольку число 2п2 четно, то число т2 должно быть четным. Но тогда будет четным и число т. (Докажите это!) Таким образом, т = 2k, где k — некоторое целое число. Подставляя это выражение для т в формулу т2 = 2п2 получаем: 4k2 = 2п2, откуда п2 =2k2. В таком случае число п2 будет четным; но тогда должно быть четным и число п. Выходит, что числа т и п четные. А это противоречит тому, что дробь m/n несократима. Следовательно, наше исходное предположение о существовании дроби m/n, удовлетворяющей условию (m/n)2 = 2., неверно. Остается признать, что среди всех рациональных чисел нет такого, квадрат которого был бы равен 2. Поэтому уравнение х2 = 2 в множестве рациональных чисел неразрешимо. Аналогичное заключение можно было бы сделать и о многих других уравнениях вида х2 = а, где а — положительное целое число. Тем не менее в VIII классе мы неоднократно говорили о корнях таких уравнений. А положительному корню уравнения х2= а мы даже дали специальное название «корень квадратный из числа а» и ввели для него специальное обозначение: √a . Итак, к рациональным числам √2 не принадлежит. А как же в таком случае можно охарактеризовать √2 ? Чтобы ответить на этот вопрос, вспомним правило для извлечения квадратных корней. Применительно к числу 2 это правило дает:
Процесс извлечения,корня в данном случае не может закончиться ни на каком шаге. В противном случае √2 был бы равен некоторой конечной десятичной дроби и потому был бы рациональным числом. А это противоречит доказанной выше теореме. Таким образом, при извлечении корня квадратного из 2 получается бесконечная десятичная дробь. Эта дробь не может быть периодической, иначе ее, как и всякую другую бесконечную периодическую дробь, можно было бы представить в виде отношения двух целых чисел. А это также находится в противоречии с доказанной выше теоремой. Таким образом, √2 можно рассматривать как бесконечную непериодическую десятичную дробь. Итак, к бесконечным непериодическим десятичным дробям нас приводит, например, действие извлечения корней из целых чисел. В последующих параграфах мы рассмотрим еще одну задачу, которая, вообще говоря, никак не связана с извлечением корней, но которая также приводит нас к бесконечным непериодическим десятичным дробям. Упражнения 305. Укажите несколько натуральных чисел, квадратные корни из которых были бы рациональными числами. 306. Докажите, что если корень квадратный из натурального числа представляет собой рациональное число, то это рациональное число является непременно целым. 307. Докажите, что уравнение х3 = 5 в множестве рациональных чисел не имеет корней. |