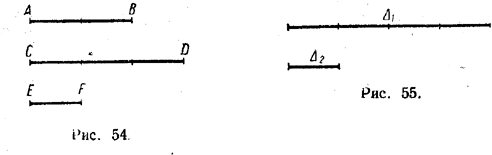
ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА  II

§ 40 Соизмеримые и несоизмеримые отрезки

Отрезок Δ называется общей мерой отрезков Δ₁ и Δ₂, если он укладывается целое число раз в каждом из этих отрезков.

Например, отрезок, EF, изображенный на рисунке 54, укладывается в АВ два раза, а в CD — 3 раза. Поэтому он является общей мерой отрезков АВ и CD. Аналогично этому, отрезок Δ₂, изображённый на рисунке 55, является общей мерой отрезкой Δ₁ и Δ₂, поскольку в Δ₁ он укладывается 4 раза, а в Δ₂ (в самом себе) — один раз.

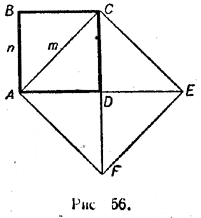
Любые ли два отрезка имеют общую  меру? Ответ на этот вопрос будет дан несколькими строками ниже. А пока мы введем еще одно определение.

Два отрезка, имеющие общую меру, называются соизмеримыми, а не имеющие   общей меры — несоизмеримыми.

Теперь вопрос о том, любые ли два отрезка имеют общую меру, можно перефразировать таким образом: любые ли два отрезка являются соизмеримыми? Следующая теорема дает отрицательный ответ на этот вопрос.

Теорема. Диагональ любого квадрата несоизмерима с его стороной.

Доказательство будем проводить методом от противного. Предположим, что диагональ АС квадрата ABCD (рис. 56) соизмерима с его стороной АВ.

Тогда существует общая мера этих отрезков, то есть отрезок, который в АВ укладывается ровно п раз, а в АС ровно т раз. Если принять этот отрезок за единицу длины, то длина АВ выразится числом п, а  длина АС — числом т.

На диагонали АС построим новый квадрат ACEF, как показано на рисунке 56. Очевидно, что площадь этого квадрата вдвое больше площади квадрата ABСD:

S_ACEF = 2S_ABСD

но

S_ABСD = n²  ,  a S_ACEF= m².

Поэтому

m² = 2n²

откуда

(^m/_n)² = 2

Но это равенство противоречит теореме, доказанной в предыдущем параграфе: «Не существует рационального числа, квадрат которого равен 2».

Следовательно, наше исходное предположение неверно. Остается признать, что диагональ любого квадрата несоизмерима с его стороной.

Теперь мы можем сделать два важных вывода.

1.  Если   отрезок   CD   соизмерим   с единицей   длины АB, то его длина выражается рациональным числом.

Действительно, в силу того что отрезки АВ и CD соизмеримы, найдется третий отрезок EF, который в АВ укладывается ровно п раз,, а в CD ровно т раз. Но в таком случае п-я часть отрезка АВ должна укладываться в CD ровно т раз.  Поэтому длина CD выражается рациональным   числом ^m/_n .

2.  Если отрезок CD несоизмерим с единицей длины АВ, то длина его не выражается никаким рациональным числом.

Действительно, если бы длина отрезка CD выражалась некоторым рациональным числом, например ^p/_q,   то    q-я    доля   отрезка АВ укладывалась бы в АВ   q  раз, а   в   CD  р  раз. Нo в  таком случае q-ю долю отрезка АВ можно было бы считать общей мерой отрезков АВ и CD. А это противоречит условию: отрезки АВ и CD несоизмеримы.

Упражнения

308. Докажите, что если отрезки АВ и CD соизмеримы, то п-я доля отрезка АВ соизмерима с т-й долей отрезка CD (m и п — произвольные натуральные числа).

309.  Докажите,   что  если  отрезки  АВ  и   CD   несоизмеримы, то п-я доля отрезка АВ несоизмерима с т-й долей отрезка CD (m и п  — произвольные натуральные числа).

310.  Пусть Δ₁ и Δ₂  — два соизмеримых отрезка, причем отрезок Δ₁ длиннее отрезка  Δ₂. Докажите,   что  в   таком  случае отрезки Δ₁ + Δ₂ и Δ₁ — Δ₂ будут также соизмеримыми.

Верно ли обратное утверждение?

311. Докажите, что в  прямоугольном треугольнике катет, лежащий против угла в 60°, несоизмерим с гипотенузой.

312. Докажите, что если отрезок АВ соизмерим с отрезком CD, а отрезок CD соизмерим с отрезком EF, то отрезок АВ соизмерим с отрезком EF.

313. Докажите, что если отрезок АВ соизмерим с отрезком CD, но несоизмерим с отрезком EF, то отрезки CD и EF несоизмеримы.

ОТВЕТЫ