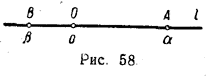
ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА  II

§ 44 Геометрическое изображение действительных чисел

Геометрически действительные числа, так же как и рациональные числа,  изображаются  точками  прямой.

Пусть l — произвольная прямая, а О — некоторая ее точка ( рис. 58 ). Каждому положительному действительному числу α поставим в соответствие точку А, лежащую справа от О на расстоянии в α единиц длины.

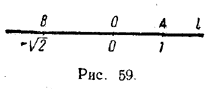
Если, например, α = 2,1356..., то

2 < α < 3
2,1 < α < 2,2
2,13 < α < 2,14

и т. д. Очевидно, что точка А в этом случае должна находиться на прямой l правее точек, соответствующих числам

2; 2,1; 2,13; ... ,

но левее точек, соответствующих числам

3; 2,2; 2,14; ... .

Можно показать, что эти условия определяют на прямой l единственную точку А, которую мы и рассматриваем как геометрический образ действительного числа α = 2,1356... .

Аналогично, каждому отрицательному действительному числу β поставим в соответствие точку В, лежащую слева от О на расстоянии в | β | единиц длины. Наконец, числу «нуль» поставим в соответствие точку О.

Так, число 1 изобразится на прямой l точкой А , находящейся справа от О на расстоянии в одну единицу длины (рис. 59), число — √2 — точкой В, лежащей слева от О на расстоянии в √2 единиц   длины, и т. д.

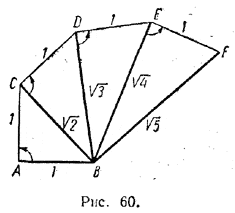
Покажем, как на прямой l с помощью циркуля и линейки можно отыскать точки, соответствующие действительным числам √2, √3, √4, √5 и т. д. Для этого прежде всего покажем, как можно построить отрезки, длины которых выражаются этими числами. Пусть АВ есть отрезок, принятый за единицу длины (рис. 60).

В точке А восставим к этому отрезку перпендикуляр и отложим на нем отрезок АС, равный отрезку АВ. Тогда, применяя теорему Пифагора к прямоугольному треугольнику  ABC,  получим; ВС = √АВ² + АС² = √1+1 = √2 

Следовательно, отрезок ВС имеет длину √2. Теперь восставим перпендикуляр к отрезку ВС в точке С и выберем на нем точку D так, чтобы отрезок CD был равен единице длины АВ. Тогда из прямоугольною треугольника BCD найдем:

ВD = √ВC² + СD² = √2+1 = √3

Следовательно, отрезок BD имеет длину √3. Продолжая описанный процесс дальше, мы могли бы получить отрезки   BE,   BF, ..., длины которых выражаются числами  √4,  √5 и т. д.

Теперь на прямой l легко найти те точки, которые служат геометрическим изображением чисел √2, √3, √4, √5 и т. д.

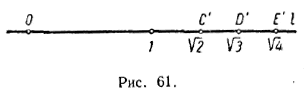
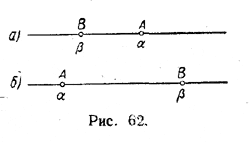
Откладывая, например, справа от точки О отрезок ВС (рис. 61), мы получим точку С, которая служит геометрическим изображением числа √2. Точно так же, откладывая справа от точки О отрезок BD, мы получим точку D', которая является геометрическим образом числа √3, и т. д.

Не следует, однако, думать, что с помощью циркуля и линейки на числовой прямой l можно найти точку, соответствующую любому заданному действительному числу. Доказано, например, что, имея в своем распоряжении только циркуль и линейку, нельзя построить отрезок, длина которого выражается числом π = 3,14 ... . Поэтому на числовой прямой l с помощью таких построений нельзя указать точку, соответствующую этому числу   Тем не менее такая точка существует.

Итак, каждому действительному числу α можно поставить в соответствие некоторую вполне определенную точку прямой l. Эта точка будет отстоять от начальной точки О на расстоянии в | α | единиц длины и находиться справа от О, если α > 0, и слева от О, если α < 0. Очевидно, что при этом двум неравным действительным числам будут соответствовать две различные точки прямой l. В самом деле, пусть числу α соответствует точка А, а числу β — точка В. Тогда, если α > β, то А будет находиться правее В (рис. 62, а); если же α < β, то А будет лежать левее В  (рис. 62,б).

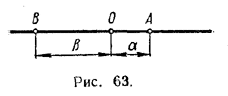
Говоря в § 37 о геометрическом изображении рациональных чисел, мы поставили вопрос: любую ли точку прямой можно рассматривать как геометрический образ некоторого рационального числа? Тогда мы не могли дать ответ на этот вопрос; теперь же мы можем ответить на него вполне определенно. На прямой есть точки, которые служат геометрическим изображением иррациональных чисел (например, √2). Поэтому не всякая точка прямой изображает рациональное число. Но в таком случае напрашивается другой вопрос: любую ли точку числовой прямой можно рассматривать как геометрический образ некоторого действительного числа? Этот вопрос решается уже положительно.

В самом деле, пусть А — произвольная точка прямой l, лежащая справа от О (рис. 63).

Длина отрезка ОА выражается некоторым положительным действительным числом α (см § 41). Поэтому точка А является геометрическим образом числа α. Аналогично устанавливается, что каждая точка В, лежащая слева от О, может рассматриваться как геометрический образ отрицательного действительного числа — β, где β — длина отрезка ВО. Наконец, точка О служит геометрическим изображением числа нуль. Понятно, что две различные точки прямой l не могут быть геометрическим образом одного и того же действительного числа.

В силу изложенных выше причин прямая, на которой указана в качестве «начальной» некоторая точка О (при заданной единице длины), называется числовой прямой.

Вывод. Множество всех действительных чисел и множество всех точек числовой прямой находятся во взаимно однозначном соответствии.

Это означает, что каждому действительному числу соответствует одна, вполне определенная   точка числовой прямой и, наоборот, каждой   точке   числовой  прямой  при   таком соответствии  отвечает одно, вполне определенное действительное число.

Упражнения

320. Выяснить, какая из двух точек находится на числовой прямой левее и какая правее, если эти точки соответствуют числам:

а)  1,454545... и 1,455454...;           в)      0 и  — 1,56673...;

б)  — 12,0003... и — 12,0002...;     г) 13,24... и 13,00....

321. Выяснить, какая из двух точек находится на числовой прямой дальше от начальной точки О, если эти точки соответствуют числам:

а) 5,2397... и 4,4996...; ..                в) —0,3567... и 0,3557... .

г) — 15,0001 и — 15,1000...;

322. В этом параграфе было показано, что для построения отрезка длиной в √n  с помощью циркуля и линейки можно поступить следующим образом: сначала построить отрезок длиной √2, затем отрезок длиной √3 и т. д., пока не дойдем до отрезка длиной √n. Но при каждом фиксированном п > 3 этот процесс можно ускорить. Как бы, например, вы стали строить отрезок длиной √10?

323*. Как  с  помощью  циркуля и линейки   найти  на  числовой прямой точку,   соответствующую числу ¹/_α, если положение  точки, соответствующей числу α, известно?