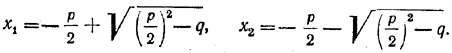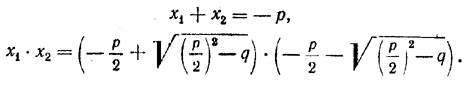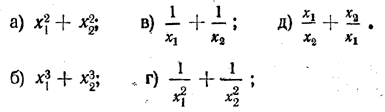КВАДРАТНЫЙ ТРЕХЧЛЕН  III

§ 52. Теорема Виета

В § 51 мы получили следующие формулы для корней приведенного квадратного уравнения с неотрицательным дискриминантом:

Из них вытекает, что

Произведение суммы двух чисел на их разность равно разности квадратов этих чисел. Поэтому

Итак,

x₁ + x₂ == — р,

x₁ • x₂ = q.

Если приведенное квадратное уравнение имеет действительные корни, то сумма их равна коэффициенту при х, взятому с противоположным знаком, а произведение—свободному члену этого уравнения.

Это свойство корней приведенного квадратного уравнения носит название теоремы Виета.  (Виет   (1540—1603) — французский   математик)

Пример. Для уравнения x² — 7х — 8 = 0   D = 81 > 0. Поэтому уравнение имеет два различных действительных корня x₁ и x₂. По теореме Виета

x₁ + x₂ = 7,         x₁ •  x₂ = — 8.

Предлагаем учащимся решить данное уравнение и убедиться в справедливости полученных нами соотношений.

Квадратное уравнение общего вида ax²  + bx + c = 0 делением на а сводится к приведенному квадратному уравнению

 x²  + ^b/_a x + ^c/_a = 0

Если исходное уравнение ax²  + bx + c = 0 имеет действительные корни x₁ и x₂, то и уравнение  x²  + ^b/_a x + ^c/_a = 0 должно иметь те же самые корни x₁ и x₂. При этом по теореме Виета должно быть

x₁ + x₂ = — ^b/_a,        x₁ •  x₂ = ^c/_a

Пример. Уравнение 2x² — 2х — 3 = 0 имеет дискриминант D = 28 > 0. Поэтому оно имеет два действительных корня x₁ и x₂, причем

x₁ + x₂ = — ^—2/₂ = 1 ,    x₁ •  x₂ =^—3/₂ = — ³/₂

Предлагаем учащимся решить данное уравнение и убедиться в справедливости полученных соотношений.

В дальнейшем нам потребуется теорема, обратная теореме Виета.  Формулируется она следующим образом.

Если существуют действительные числа x₁ и x₂ такие, что

x₁ + x₂  = — р,          x₁ • x₂ = q,

то эти числа (x₁ и x₂ ) являются корнями квадратного уравнения  

x²  + px + q = 0 .

Доказательство. Если x₁ + x₂  = — р, то x₂ = — р — x₁. Подставляя это выражение для x₂ в соотношение x₁ • x₂ = q, получаем:

x₁ • (— р — x₁) = q,      — px₁ — x₁² = q,          x₁² + px₁ + q =  0.

Но это означает, что число  x₁ является корнем уравнения x²  + px + q = 0. Аналогично доказывается, что корнем этого уравнения является и число x₂. Впрочем, это и так ясно: ведь числа x₁ и x₂ входят в формулировку нашей теоремы совершенно симметрично.

Упражнения

383. (Устно.)   Решить  уравнения:

1)  x²  — 3x + 2 = 0;                    5) — x²  — 7x + 8 = 0;

2)  x²  + 99x — 100 = 0;               6) x²  — 7x + 12 = 0;

3)  x²  + 548x — 549 = 0;              7) 3x²  + x — 2 = 0;

4)  — x²  + 6x — 5 = 0;                 8) x²  — 5x + 6 = 0.

384. Обозначим через x₁ и x₂  корни уравнения

x²  — 7x + 10 = 0.

Не находя этих корней, определить:

385.   То же, что и в задаче 384, сделать для уравнения

— 3x² + х + 24 = 0.

386.   При каких значениях х выражение (х — 1) (х + 5) равно  (a — 1) (a + 5)?

387.  Доказать, что корни уравнения ax²  + bx + a = 0 (если только они  существуют)  представляют собой взаимно обратные числа.

388. Определить число т так, чтобы уравнение

x² — 12x + т = 0

имело два действительных корня, один из которых больше другого на 2√5.

389.  Определить   число а так,   чтобы  один из   корней  уравнения

4x² — 15x + 4а³ = 0

был квадратом другого.

390.   При каких значениях а уравнение

x² — 4х + а = 0      имеет:

а)   действительные  корни;

б)  действительные  корни одного знака;

в)  действительные корни разных знаков;

г)  один корень нулевой, а другой — положительный;

д)  один корень нулевой, а другой — отрицательный?

ОТВЕТЫ