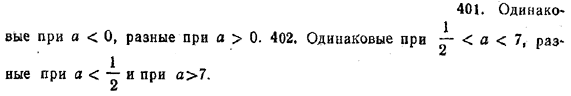КВАДРАТНЫЙ ТРЕХЧЛЕН  III

§ 53. Исследование знаков корней квадратного уравнения по его коэффициентам

Используя теорему Виета, можно, не решая уравнения x²  + px + q = 0. определить, какими будут его корни: положительными или отрицательными. Но при этом, конечно, нужно быть уверенным в том, что рассматриваемое уравнение имеет корни. Если же корней нет, то говорить о знаках корней не имеет смысла. Поэтому на протяжении всего этого параграфа мы будем предполагать, что рассматриваемое приведенное квадратное уравнение x²  + px + q = 0 имеет корни, то есть дискриминант его неотрицателен.

1)   Пусть q > 0; тогда оба корня имеют одинаковые знаки, поскольку x₁ • х₂= q > 0.
Если к тому же р < 0, то x₁ + х₂ = — р > 0,  значит,  оба  корня    положительны.
Если    р > 0, то x₁ + х₂ = — р < 0, и тогда оба корня отрицательны.
В случае, когда р = 0, уравнение, не будет иметь действительных корней, потому что сумма двух положительных или двух отрицательных чисел не может быть равна нулю.

2)  Предположим теперь, что q < 0. Тогда один из корней должен быть положительным, а другой — отрицательным,  поскольку x₁ • х₂= q <  0.
Если  при  этом   р > 0,   то x₁ + х₂ = — р < 0, и, значит, абсолютная величина отрицательного корня больше положительного корня.
Если же р < 0, то x₁ + х₂ = — р > 0.   Это возможно  только  тогда,   когда   положительный   корень   больше абсолютной  величины    отрицательного    корня.
При    р = 0    x₁ + х₂  = 0, откуда x₁= — х₂ в этом случае корни равны по абсолютной величине и противоположны по знаку.

3)  Осталось рассмотреть случай, когда q = 0. Тогда x₁ • х₂ = 0, поэтому хотя бы один из корней равен нулю.
Пусть для определенности x₁ = 0, тогда другой корень найдется из условия x₁ + х₂ = — р, откуда х₂ = — р. Значит, в этом случае один корень равен нулю, а другой представляет собой число, противоположное коэффициенту р.
Если же и р = 0, то уравнение имеет , два равных корня: x₁= х₂ = 0.

Полученные результаты исследования знаков корней представлены в таблице .

Еще раз отметим, что приведенные здесь рассуждения верны лишь в предположении, что исследуемое уравнение имеет действительные корни,  то есть его дискриминант неотрицателен.

Рассмотрим несколько примеров на исследование знаков корней  квадратных   уравнений.

1) x²  — 8х — 9 = 0. Дискриминант этого уравнения равен D = 64 + 36 = 100 > 0. Поэтому уравнение имеет два различных действительных корня.
Вследствие того, что x₁ • х₂ = — 9, корни должны иметь разные знаки,
а так как x₁ + х₂  = 8, то абсолютная величина отрицательного корня меньше положительного  корня.

2) x²  + 7х + 10 = 0.  Дискриминант этого   уравнения  равен D = 49 — 40 = 9 > 0. Поэтому уравнение имеет два различных действительных корня.
Так как x₁ • х₂ = 10 > 0, то корни имеют одинаковые знаки.
Кроме того, x₁ + х₂ = —7, значит, оба корня отрицательны.

3)  x² — х + 1 = 0.  Для данного  уравнения

D = (—1)² — 4 = — 3 < 0.

Следовательно, это уравнение не имеет действительных корней. Полученные выше результаты относятся лишь к приведенным квадратным уравнениям. Но подобные исследования можно провести и для любых квадратных уравнений ax²  + bx + c = 0 . Для этого сначала нужно посредством деления на а привести данное уравнение к  приведенному  квадратному   уравнению x² + ^b/_a х +  ^c/_a = 0, а затем для этого уравнения провести описанные выше рассуждения.

Пусть,  например,  нужно исследовать знаки  корней  уравнения —3x² + 5х — 2 == 0. Дискриминант этого уравнения равен  D = 25 — 24 = 1 > 0. Поэтому оно имеет два различных действительных корня.

Разделив обе части уравнения на — 3,   получим:   x²— ⁵/₃х + ²/₃ = 0.   Отсюда   видно,    что корни  данного уравнения имеют одинаковые знаки, так как x₁ • х₂ = ²/₃ > 0. Кроме того, x₁ + х₂ = ⁵/₃ > 0. Следовательно, оба корня положительны.

Упражнения

Не решая данных уравнений (№ 391—400), определить знаки их корней:

Проверить себя, да и вообще исследовать квадратные уравнения полные и приведенные можно, с помощью соответствующих алгоритмов в программе EXCEL. Алгоритм можно  усовершенствовать  для отображения промежуточных результатов вычислений.

391. x² — 4х + 3 = 0.            396. 6x² — х  — 1 == 0.

392. x² — 6х  + 5 = 0.          397. —20x² — 3х  + 2 = 0.

393. x² — х  — 42 = 0.         398. x² — 6х  + 10 = 0.

 394. x² — х  — 6 = 0.          399. — 3x² +17 = 0.

395. x² + х  + 1 = 0.              400. —5x² + х  — 7 = 0.

401. При каких значениях а корни уравнения

x² + (1 — а) х — а = 0

имеют одинаковые знаки и при каких — разные?

402. При каких значениях а корни уравнения

x² + (а + 6)х + (2а — 1) (7 — а) = 0

имеют одинаковые знаки и при каких — разные?

ОТВЕТЫ