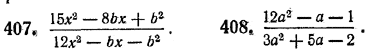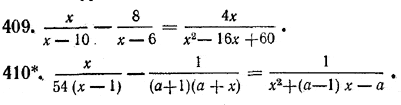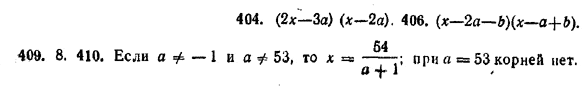КВАДРАТНЫЙ ТРЕХЧЛЕН  III

§ 54. Разложение квадратного трехчлена на линейные множители

В этом параграфе мы рассмотрим следующий вопрос: в каком случае квадратный трехчлен ax²  + bx + c можно представить в   виде   произведения

(a₁x + b₁) (a₂x + b₂)

двух линейных  относительно х множителей  с действительными коэффициентами     a₁, b₁, a₂, b₂     (a₁ =/=0, a₂ =/=0) ?

1.  Предположим, что данный квадратный трехчлен ax²  + bx + c  представим в виде

ax²  + bx + c  = (a₁x + b₁) (a₂x + b₂).                   (1)

Правая часть формулы (1) обращается в нуль при  х =  —  b₁/ a₁ и х = —  b₂/ a₂  (a₁и a₂ по условию не равны нулю). Но в таком случае числа  —  b₁/ a₁ и  —  b₂/ a₂   являются корнями уравнения

ax²  + bx + c = 0.

Следовательно, дискриминант квадратного трехчлена ax²  + bx + c должен  быть  неотрицательным.

2.  Обратно,   предположим,   что   дискриминант  D = b² — 4ас квадратного трехчлена ax²  + bx + c  неотрицателен.  Тогда этот трехчлен имеет действительные корни x₁ и x₂. Используя    теорему Виета,  получаем:

ax²  + bx + c  = а (x² + ^b/_a х + ^c/_a) = а [x² — (x₁ + x₂) х + x₁x₂] =

= а [(x²— x₁x ) — (x₂x — x₁x₂)] = а [х (х — x₁) — x₂(х — x₁) =

= a(х — x₁)(х — x₂).

Итак,

ax²  + bx + c = a(х — x₁)(х — x₂),                 (2)

где x₁ и x₂ — корни трехчлена ax²  + bx + c. Коэффициент а можно отнести к любому из двух линейных множителей,  например,

a(х — x₁)(х — x₂) = (aх — ax₁)(х — x₂).

Но это означает, что в рассматриваемом случае квадратный трехчлен ax²  + bx + c представим в виде произведения двух линейных множителей с действительными коэффициентами.

Объединяя результаты, полученные в пунктах 1 и 2, мы приходим к следующей теореме.

Теорема. Квадратный трехчлен ax²  + bx + c тогда и тoлько тогда можно представить в виде произведения двух линейных множителей с действительными коэффициентами,

ax²  + bx + c = (aх — ax₁)(х — x₂),

когда дискриминант этого квадратного трехчлена неотрицателен (то есть когда этот трехчлен имеет действительные корни).

Пример 1.   Разложить на линейные множители 6x² — х —1.

Корни этого квадратного трехчлена равны x₁ = ¹/₂  и x₂ = — ¹/₃.

Поэтому по формуле (2)

6x² — х —1 = 6 (х — ¹/₂)(х + ¹/₃) = (2х — 1) (3x + 1).

Пример 2.  Разложить на линейные множители x² + х + 1. Дискриминант    этого    квадратного    трехчлена    отрицателен:

D = 1² — 4•1•1 = — 3 < 0.

Поэтому данный  квадратный трехчлен  на линейные множители с действительными  коэффициентами   не раскладывается.

Упражнения

Разложить   на   линейные   множители   следующие  выражения (№ 403 — 406):

403. 6x² — 7х + 2.                  405. x² — х + 1.

404.   2x² — 7ах + 6а².             406. x² — 3ах + 2а² — аb— b².

Сократить дроби  (№ 407,  408):

Решить   уравнения:

ОТВЕТЫ