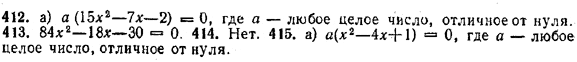КВАДРАТНЫЙ ТРЕХЧЛЕН  III

§ 55. Составление квадратного уравнения по заданным корням

Предположим, что нам нужно составить квадратное уравнение, корнями которого были бы числа x₁ и x₂. Очевидно, что в качестве  искомого  уравнения   можно  выбрать  уравнение

a(х — x₁)(х — x₂) = 0,                      (1)

где а — любое отличное от нуля действительное число. С другой стороны, как было показано в § 54, каждое квадратное уравнение с корнями x₁ и x₂ можно записать в виде (1).

Таким образом, формула (1) полностью решает поставленную выше задачу. Из всех квадратных уравнений корни x₁ и x₂ имеют уравнения вида (1) и только, они.

Пример. Составить квадратное уравнение, корни которого равны  1  и — 2.

Ответ.   Корни 1 и —2 имеют все квадратные уравнения вида

а(х — 1)(х + 2) = 0,

или

ах² + ах — 2а = 0,

где а — любое отличное от нуля действительное число. Например,   при   а = 1   получается   уравнение

х² + х — 2 = 0.

Упражнения

411.  Составить квадратное уравнение, корнями которого были бы  числа:

а) 2 и — 3;    б) — 1 и — 5;      в) ¹/₄ и ¹/₆;    г) — ¹/₂ и — ¹/₃ .

412.  Составить квадратное уравнение с целыми коэффициентами так, чтобы его корни были равны:

а) — ¹/₅   и  ²/₃;    б) ⁴/₇  и 5;    в) — ³/₂  и  ²/₉;    г) — ³/₁₀  и — ²/₅.

413.   Составить квадратное уравнение с целыми  коэффициентами, корни которого равны ⁵/₇ и — ¹/₂, а сумма всех коэффициентов равна 36.

414.  Могут ли  корнями  квадратного уравнения с натуральными коэффициентами   быть  числа ⁶/₅ и — ¹/₇?

415.  Составить квадратное уравнение с целыми  коэффициентами, если известно, что один из его корней равен:

а) 2 + √3 ;       б) 3 —√2 .

ОТВЕТЫ