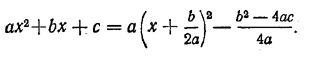КВАДРАТНЫЙ ТРЕХЧЛЕН  III

§ 57. График квадратной функции

В этом параграфе мы покажем, как строится график квадратной функции у = ax²  + bx + c. Наше рассмотрение придется разбить на ряд отдельных этапов.

1. График функции  у = x².   

Этот   график   строится   «по   точкам». Составим следующую таблицу значений функции:

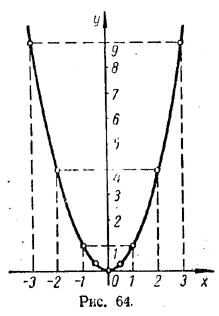
Отметим соответствующие точки на плоскости координат и соединим их плавной кривой (рис. 64). Эта кривая называется параболой. На рисунке 64 парабола у = x² начерчена лишь при —3 < х < 3. При | х |> 3 она уходит (и притом весьма круто) все выше  и  выше.

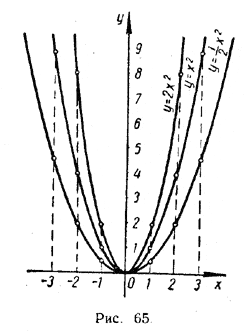
Парабола у = x²  обладает следующими основными свойствами.

1) Она лежит целиком в верхней полуплоскости. Это соответствует тому, что функция у = x²  принимает только неотрицательные значения. В начале координат парабола касается оси абсцисс. Это самая низкая точка графика; она называется вершиной параболы.

2) Парабола симметрична относительно оси ординат. Если перегнуть рисунок 64 по оси у, то левая и правая части параболы совместятся. Это служит графической иллюстрацией того, что функция у = x²  не меняет своих значений при изменении знака у аргумента:

(— x)² =  x²

Такие функции называются четными.

2. График функции у = αx².

График функции у = αx², так же как и график функции у = x², легко строится «по точкам».

Сначала рассмотрим случай, когда α > 0. На рисунке 65 представлены графики  функций   у = αx²  при α = ¹/₂;  1; 2.    

Во всех этих случаях получаются кривые, симметричные относительно оси ординат и расположенные целиком в  верхней полуплоскости. Каждая из этих кривых направлена вверх. Эти кривые, так же как и кривая у = x², называются параболами. Начало координат является их общей вершиной, а ось ординат — их общей осью симметрии. Из рисунка 65 видно, что, чем больше α, тем круче ветви параболы у = αx²; чем меньше α,  тем они  положе.

Теперь рассмотрим случай,  когда α < 0.  На рисунке 66 представлены кривые  у = αx²   при   α = — ¹/₂; —1; —2. Эти направленные вниз кривые также называются параболами. Общая вершииа —начало координат — является их наивысшей точкой. Ось ординат для каждой из этих кривых служит осью симметрии. Чем больше абсолютная величина α, тем круче ветви параболы; чем она меньше, тем положе ветви  параболы.

3. График функции у = α(х — β)².

Сравним между собой две функции: у₁ = α(х — β)² и у₂ = αx², где β > 0.

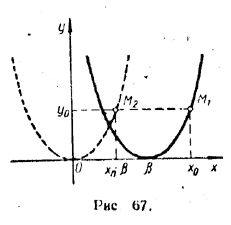
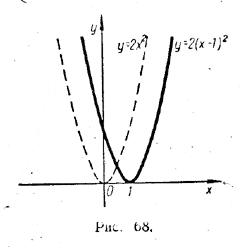
Пусть М₁ —произвольная точка графика первой функции (рис. 67). Тогда ее координаты (x₀ , y₀) связаны соотношением у₀ = α(х₀ — β)².

Но это соотношение показывает, что точка М2 с координатами (х₀ — β, y₀) должна принадлежать графику второй функции. Значит, каждая точка кривой у = α(х — β)² получается из соответствующей точки кривой у = αx² (см. рис. 67) посредством переноса    (или  смещения)   вправо  по направлению оси х на расстояние β. Поэтому и вся кривая у = α(х — β)² получается посредством переноса кривой  у = αx²  вправо на  β.

Например, кривая у = 2(х—1)² получается из кривой у = 2x², если последнюю сместить на 1 вправо (рис. 68).

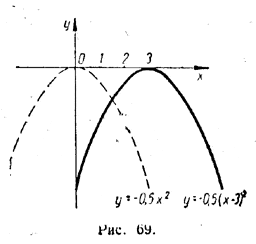
кривая у = —0,5 (х—3)²  получается смещением кривой  у = —0,5 х² вправо на 3 единицы (рис.   69).

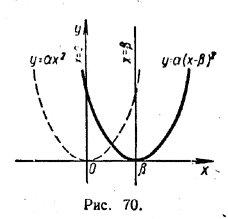
Вершиной параболы у = αx² является точка .с координатами (0, 0), а осью симметрии — прямая х = 0. При смещении вправо по направлению оси х на расстояние β точка с координатами (0, 0) переходит в точку с координатами (β, 0), а прямая х = 0 — в прямую х = β (рис. 70). Поэтому вершиной параболы у = α(х — β)² будет точка с координатами (β, 0), а осью симметрии — прямая  х = β.

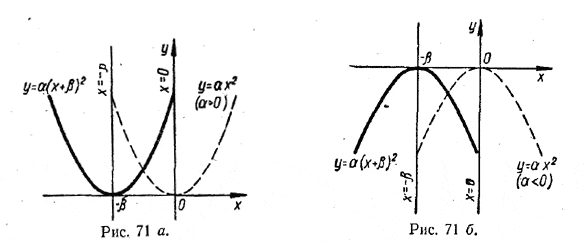
Парабола у = αx² направлена вверх при α > 0 и вниз при α < 0. Поэтому такое же направление будет иметь и парабола у = α(х — β)² .'

Итак, графиком функции у = α(х — β)²  является парабола, направленная вверх, если α > 0 и вниз при α < 0. Вершиной этой параболы является точка с координатами (β, 0), а осью симметрии — прямая х = β.

Точно так же может быть построен и график функции у = α(х + β)², где β > 0.

Он представляет собой параболу, которая получается посредством смещения параболы у = αx² влево на β . Эта парабола направлена вверх,если α > 0 (рис. 71а), и вниз, если α < 0 (рис. 71б). Вершина ее находится в точке с координатами (— β,   0); осью симметрии служит прямая х = — β.

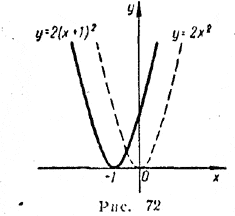
На рисунке 72 вы видите график функции у = 2(х + 1)². Он получен посредством параллельного переноса параболы у = 2х² влево на 1.

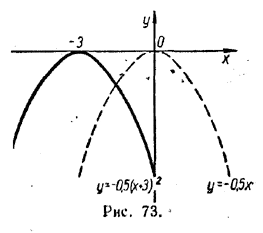
График функции у  = —0,5 (х + 3)² (рис. 73) получен посредством параллельного переноса параболы у =—0,5х²  влево на  3.

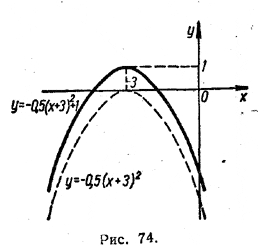
4.  График функции  у = α(х — β)² + γ       Этот     график     получается    посредством   смещения параболы у = α(х — β)² по направлению оси  у  вверх на   расстояние γ , если γ  > 0, и вниз на расстояние — γ , если   γ  < 0.   В   результате     смещения     получается парабола с вершиной в точке, координаты   которой   равны   (β, γ ). Осью   симметрии   такой параболы служит  прямая  х = β.

При смещении вверх или вниз плраболу у = α(х — β)² не меняет своего направления. Поэтому параболы  у = α(х — β)² + γ  и  у = α(х — β)² имеют одно и то же направление: при α > 0 — вверх, a при  α < 0 — вниз.

В качестве примера на рисунке 74 представлен график функции у  = —0,5 (х + 3)² + 1, который получается смещением графика   у  = —0,5 (х + 3)² вверх на 1.

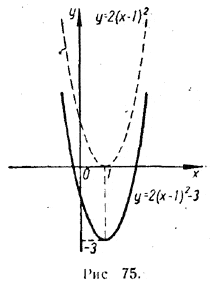
На рисунке 75 вы видите график функции у = 2(х + 1)² —3, полученный из графика у = 2(х + 1)² смещением вниз на 3 по оси симметрии.

Все вышеуказанные исследования функции у = α(х — β)² + γ  можно провести и в программе Excel .

5.  График функции у = ax²  + bx + c.

Как отмечалось в § 49, квадратный трехчлен ax²  + bx + c представим  в  виде

Последнее выражение имеет вид  у = α(х — β)² + γ ,   где

Поэтому графиком функции у = ax²  + bx + c является парабола с вершиной в точке

Осью симметрии этой параболы является прямая х = — ^b/_2a . При а > 0 парабола направлена вверх, а при а < 0 — вниз.

Исследовать график функции у = ax²  + bx + c   можно  в программе Excel