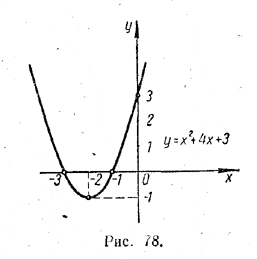
КВАДРАТНЫЙ ТРЕХЧЛЕН  III

§ 59. Характеристические точки параболы

Характеристическими точками параболы у = ax²  + bx + c  мы называем ее вершину и точки пересечения с осями координат.

Вершину имеет любая парабола у = ax²  + bx + c . Координаты этой вершины легко найти, выделив в квадратном трехчлене ax²  + bx + c  полный квадрат (см. § 49). Например, для параболы  у = x² + 4x +3   имеем:

x² + 4x +3 = (х + 2)² — 1.

Поэтому абсцисса вершины равна —2, а ордината —1   (рис.  78).

Точку пересечения с осью у имеет также любая парабола у = ax²  + bx + c . Абсцисса точки пересечения равна, очевидно, нулю, а ордината с. Она получается, если в выражении ax²  + bx + c  положить х = 0.

Например, точка пересечения параболы у = x² + 4x +3 с осью ординат (рис. 78) имеет координаты (0,3).

Точки пересечения с осью х . имеет не всякая парабола у = ax²  + bx + c . Если дискриминант D = b² — 4ас положителен, то уравнение ax²  + bx + c = 0 имеет два различных   действительных   корня:

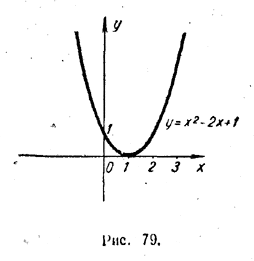
В этом случае парабола у = ax²  + bx + c  пересекает ось х в двух точках с абсциссами x₁ и x₂ соответственно.

Так, для квадратного трехчлена  x² + 4x +3     D = 16 — 12 = 4 > 0. Этот квадратный трехчлен имеет два корня: x₁ = —1 , x₂ = —3. Поэтому парабола у = x² + 4x +3  пересекает ось x в двух точках (рис. 78),  абсциссы которых равны — 1 и — 3.

Если D = b² — 4ас = 0, то уравнение ax²  + bx + c = 0 имеет   один  действительным корень х  =  — ^b/_2a

В этом случае уравнений параболы можно записать в виде у = а (х + ^b/_2a )²

Такая парабола касается оси х в точке с абсциссой — ^b/_2a

Например, для квадратного трехчлена  x² —2х + 1    D = 0. Уравнение x² —2х + 1 = 0 имеет один корень: х = 1. Поэтому парабола у = x² —2х + 1 касается оси х в точке с абсциссой 1 (рис.   79).

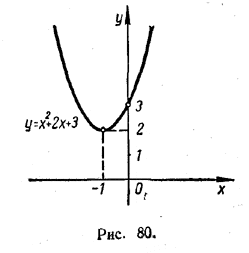
Если D = b² — 4ас  < 0, то уравнение ax²  + bx + c = 0 не имеет действительных корней. В этом случае парабола не пересекает оси х. Например, для квадратного трехчлена    x² +2х+ 3   D = — 8 < 0. Уравнение x² +2х + 3 =0  не имеет действительных корней. Парабола у =  x² +2х+ 3 не пересекает оси х (рис. 80).

Характеристические точки параболы всегда полезно находить при построении графика функции у = ax²  + bx + c . Это позволяет более точно построить график.

Упражнения

Начертить данные параболы, указав координаты характеристических точек и уравнения осей симметрии:

428.   у = 3(х — 2)² — 2.              431. у = 2х² — 2х — 4.

429.  у = — (х + 1)² + 3.               432. у = х² + 12х + 22.

430.   у = 3 — 2х — х².                433. у = х(1 — х).