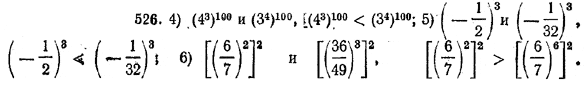СТЕПЕНЬ С РАЦИОНАЛЬНЫМ ПОКАЗАТЕЛЕМ,

СТЕПЕННАЯ ФУНКЦИЯ  IV

§ 70. Сравнение степеней

Теорема 1. Из двух степеней с одинаковыми показателями и положительными основаниями больше та, основание которой больше. Другими словами, если а > b > 0, то при любом натуральном п

аⁿ > bⁿ.

Это свойство было доказано нами в главе I (§ 12).

Пример.   Какое число больше: 2³⁰⁰ или 3²⁰⁰ ?

Для решения этой задачи представим данные числа в виде степеней  с  одинаковыми   показателями,    используя    тождество

а^mn = (а^m)ⁿ.

Имеем:

2³⁰⁰ = 2^3•100 = (2³)¹⁰⁰ =8¹⁰⁰      3²⁰⁰ = 3^2•100 = (3²)¹⁰⁰ = 9¹⁰⁰

Так как 9 > 8, то 9¹⁰⁰   > 8¹⁰⁰ . Следовательно,

3²⁰⁰  > 2³⁰⁰

Теорема 2. Если 0 < а < 1, то из двух степеней а^m и аⁿ больше та, показатель которой меньше.

Если а >1, то из двух степеней а^m и аⁿ больше та, показатель которой больше.

Доказательство. Пусть m > п. Тогда т = п + k, где k — некоторое натуральное число.  Поэтому

а^m = а^n+k =аⁿа^k.

Если 0 < а < 1, то 0 < а^k < 1. Следовательно, а^m = аⁿ • а^k < аⁿ.

Если же а > 1, то а^k > 1.   Следовательно, а^m = аⁿ • а^k > аⁿ.

Например, ( ¹/₃ )¹⁰⁰ <  ( ¹/₃ )⁵⁰;     3¹⁰⁰ > 3⁵⁰

Упражнения

526. Данные     выражения    представить  в  виде    степеней   с одинаковыми показателями и сравнить их по величине:

1) 4² и 2⁸;              4) 4³⁰⁰ и 3⁴⁰⁰;                     6) ( — ⁶/₇ )⁴  и (³⁶/₄₉)⁶;

2)  27³  и  9⁶ ;        5) — ¹/₈   и   (—¹/₃₂)³;                    7) (¹/₁₆)¹⁰⁰  и (¹/₂)⁵⁰⁰ .

3)  125² и 25³;

527. Данные   выражения     представить   в    виде    степеней   с одинаковыми основаниями и сравнить их по величине:

1)  8⁵ и 16³;                                 3) (—3)⁷⁵ и (—27)¹⁵;

2)  4¹⁰⁰ и 32⁵⁰;                              4) 81¹⁵⁰ • 8²⁰⁰   и  3⁶⁰⁰ • 16⁷⁵.

528. Что больше: (аⁿ)^m или (а^m)ⁿ?

ОТВЕТЫ