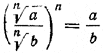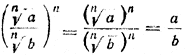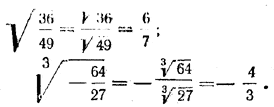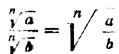|
|
СТЕПЕНЬ С РАЦИОНАЛЬНЫМ ПОКАЗАТЕЛЕМ, СТЕПЕННАЯ ФУНКЦИЯ IV § 79. Извлечение корней из произведения и частного Теорема 1. Корень п-й степени из произведения положительных чисел равен произведению корней п-й степени из сомножителей, то есть при а > 0, b > 0 и натуральном п n√ab = n√a • n√b . (1) Доказательство. Напомним, что корень п-й степени из положительного числа ab есть такое положительное число, п-я степень которого равна ab. Поэтому доказать равенство (1) — это все равно, что доказать равенство (n√a • n√b )n = ab. По свойству степени произведения (n√a • n√b )n = (n√a )n • ( n√b )n =. Но по определению корня п-й степени (n√a )n = а, ( n√b )n = b. Поэтому (n√a • n√b )n = ab. Теорема доказана. Требование а > 0, b > 0 существенно лишь для четного п, поскольку при отрицательных а и b и четном п корни n√a и n√b не определены. Если же п нечетно, то формула (1) справедлива для любых а и b (как положительных, так и отрицательных). Примеры: √16 • 121 = √16 • √121 = 4 • 11 = 44. 3√—125 • 27 = 3√—125 • 3√27 = —5•3 = — 15 Формулу (1) полезно использовать при вычислении корней, когда подкоренное выражение представляется в виде произведения точных квадратом. Например, √1532 —722 = √ (153+ 72) (153—72) = √225•81= 15 • 9 = 135. Теорему 1 мы доказали для случая, когда под знаком радикала в левой части формулы (1) стоит произведение двух положительных чисел. На самом же деле эта теорема верна для любого числа положительных сомножителей, то есть при любом натуральном k > 2:
Следствие. Читая это тождество справа налево, мы получаем следующее правило умножения корней с одинаковыми .показателями;
Чтобы перемножить корни с одинаковыми показателями, достаточно перемножить подкоренные выражения, оставив показатель корня прежним. Например, √3 • √8 • √6 = √3• 8• 6 = √144 = 12. Теорема 2. Корень п-й степени из дроби, числитель и знаменатель которой — положительные числа, равен частному от деления корня той же степени из числителя на корень той же степени из знаменателя, то есть при а > 0 и b > 0
Доказать равенство (2)—это значит показать, что
По правилу возведения дроби в степень и определению корня n-й степени имеем:
Тем самым теорема доказана. Требование а > 0 и b > 0 существенно лишь при четном п. Если же п нечетно, то формула (2) верна и для отрицательных значений а и b. Примеры:
Следствие. Читая тождество
Чтобы разделить корни с одинаковыми показателями, достаточно разделить подкоренные выражения, оставив показатель корня прежним. Например,
Упражнения 554. В каком месте доказательства теоремы 1 мы использовали то, что а и b положительны? Почему при нечетном п формула (1) верна и для отрицательных чисел а и b? При каких значениях х верны данные равенства (№ 555—560): 555. √x2 — 9 = √x —3 • √х + 3. 556. 4√(x — 2) (8 — x) = 4√х — 2 • 4√8 — x 557. 3√(х + 1) (х — 5) = 3√х +1 • 3√х — 5. 558. √х (х + 1) (х + 2) = √х • √ (х + 1) • √ (х + 2) 559. √(х — а)3 = (√х — а )3. 560. 3√(х — 5)2 = (3√х — 5)2. 561. Вычислить: a) √1732 — 522 ; в) √2002 — 562 ; б) √3732 — 2522 ; г) √242,52 — 46,52 . 562. В прямоугольном треугольнике гипотенуза равна 205 см, а один из катетов 84 см. Найти другой катет. 563. Во сколько раз:
ОТВЕТЫ 555. х > 3. 556. 2 < х < 8. 557. х — любое число. 558. х > 0. 559. х > а. 560. х — любое число. 563. а) В три раза. |
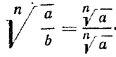 (2)
(2)