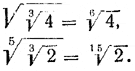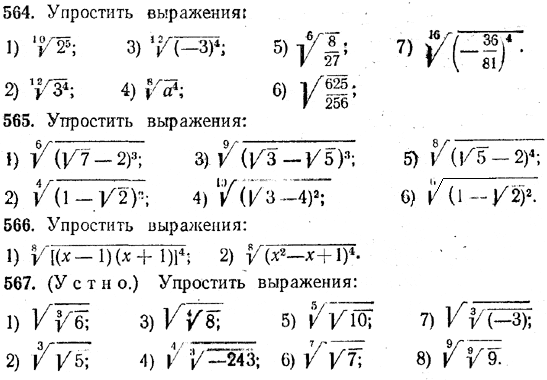|
|
СТЕПЕНЬ С РАЦИОНАЛЬНЫМ ПОКАЗАТЕЛЕМ, СТЕПЕННАЯ ФУНКЦИЯ IV § 80. Извлечение корня из степени. Пусть а — произвольное положительное число, а т и п — натуральные числа, причем т делится без остатка на п. Тогда
Например, 3√56 = 52 = 25; 4√312 = 33 = 27. Другими словами, верна следующая теорема. Теорема 1. Чтобы извлечь корень из степени положительного числа, показатель которой делится нацело на показатель корня, достаточно показатель подкоренного выражения разделить на показатель корня, оставив основание степени прежним. Доказательство. На основании правила возведения степени в степень имеем:
Но это и означает, что Теорема 2. Чтобы корень из положительного числа возвести в степень, достаточно возвести в эту степень подкоренное число, оставив показатель корня без изменения, то есть при а > 0 (n√a)m= n√am . (2) Действительно,
Если п — нечетное число, то формула (2) верна и для а < 0. Примеры: (4√2)3= 4√23 = 4√8 ; (6√16)3 = 6√163 = 6√212 =22 = 4; (3√— 2)5= 3√— 25 = 3√— 32. Теорема 3. Величина корня из положительного числа не изменится, если показатели корня и подкоренного выражения умножить на одно и то же натуральное число или разделить на их общий множитель. Другими словами: 1) если а > 0 и т, п, k — натуральные числа, то n√am = nk√amk (3) 2) если а > 0 и k — общий делитель чисел т и п, то
Доказать формулу (3) — это значит показать, что ( nk√amk )n = am. По правилу возведения корня в степень ( nk√amk )n = nk√amkn Показатель mnk степени делится нацело на показатель nk корня. Следовательно, но теореме 1 nk√amkn = am. Поэтому ( nk√amk )n = am. Это и означает, что n√am = nk√amk . Формула (4) легко вытекает из (3), Предлагаем учащимся самостоятельно убедиться в этом. Примеры. 4√3= 8√32 ; 3√22 = 9√26 ; 15√a10 = 3√a2 Теорема 4. Чтобы извлечь корень из корня, достаточно перемножить показатели этих корней, не изменяя подкоренного числа, то есть
Доказательство. По теореме ( nm√a )n = nm√a n . Величина корня не изменится, если показатель корня и показатель подкоренного числа разделить на их общий множитель (теорема 3); поэтому nm√a n = m√a . Итак, ( nm√a )n = m√a . Но по определению корня это и означает, что Например, Упражнения
ОТВЕТЫ
|
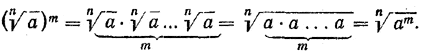
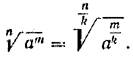 (4)
(4)