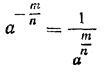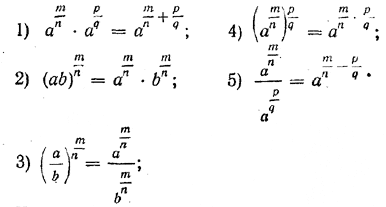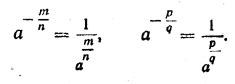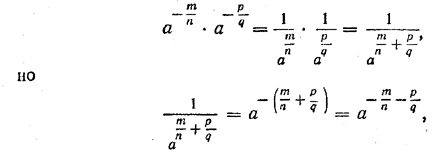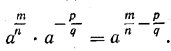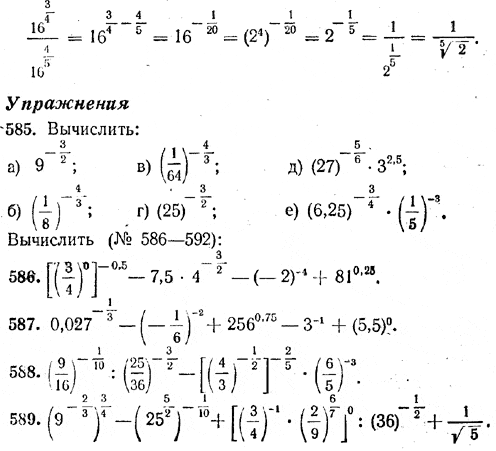СТЕПЕНЬ С РАЦИОНАЛЬНЫМ ПОКАЗАТЕЛЕМ,

СТЕПЕННАЯ ФУНКЦИЯ  IV

§ 86. Степень положительного числа с отрицательным дробным показателем

Подобно тому как в § 71 мы определили степень а^—п числа а с отрицательным целым   показателем — п, можно   определить  и степень  положительного числа а с отрицательным дробным показателем —^m/_n.

Пусть а— произвольное положительное  число,   а т и п — натуральные числа. Тогда по определению

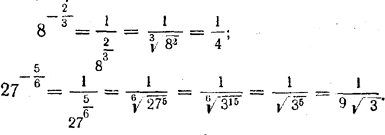
Степень положительного числа с отрицательным дробным, показателем равна единице, деленной на степень того же числа с  показателем,  противоположным   показателю   данной   степени.

Например,   

Теперь мы знаем, что представляет собой степень положительного числа с любым рациональным показателем.

Степени с рациональными показателями обладают следующими основными  свойствами:

Частично эти свойства были доказаны нами в предыдущих параграфах, но лишь для положительных показателей. Теперь же мы можем доказать их для произвольных рациональных показателей.

Докажем,  например,  свойство   1.

Для положительных показателей ^m/_n и ^p/_q доказательство было дано в  предыдущем  параграфе. Поэтому нам нужно  рассмотреть следующие случаи:

1)  оба показателя отрицательны;

2)  один из  показателей отрицательный,   а другой — положительный;

3)  хотя бы один из показателей равен нулю.

Пусть т, п, р и q — натуральные числа. Покажем, что

Действительно, по определению степени с отрицательным показателем

Поэтому

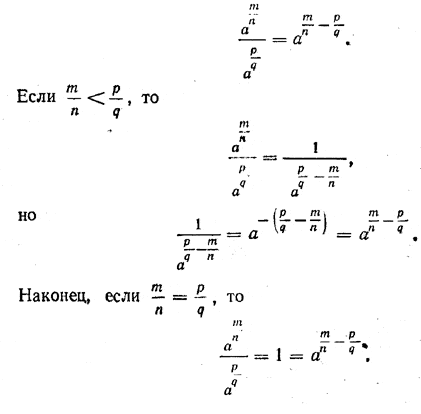
откуда и вытекает требуемое соотношение.

Мы рассмотрели случай, когда показатели каждой из двух степеней отрицательны. Теперь рассмотрим случай, когда один из них положителен, а другой отрицателен. Докажем, например,  что

Если ^m/_n > ^p/_q, то по свойству 5, упомянутому в предыдущем  параграфе,

Здесь мы используем определение а⁰ = 1. Таким образом,

Нам осталось рассмотреть случай, когда из двух степеней с одинаковыми основаниями хотя бы одна имеет нулевой показатель.. Докажем,   например,   что

Действительно,   а⁰ = 1 и ^m/_n+ 0 = ^m/_n Поэтому

Свойство   1  доказано.

Аналогично можно доказать и все остальные свойства. Заметим,   что  если   в   предыдущем   параграфе   мы   могли    говорить о свойстве 5 лишь при ^m/_n > ^p/_q,   то теперь,    используя   определения степени положительного числа с нулевым и отрицательным дробным показателем, мы можем доказать его и для случая, когда ^m/_n < ^p/_q

Например,

ОТВЕТЫ