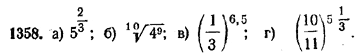ПОКАЗАТЕЛЬНАЯ И ЛОГАРИФМИЧЕСКАЯ ФУНКЦИИ   VIII

§ 174.   Степень положительного числа
с положительным рациональным показателем.

В главе IV (часть I) было дано определение степени положительного числа а с рациональным показателем r. Напомним это  определение.

Если число r — натуральное, то а^r есть произведение r чисел, каждое из которых равно а:

          (1)

Если число r — дробное и положительное, то есть r = ^m/_n ,   где m и  п — натуральные числа,  то

       (2)

Формулы (1) и (2) определяют степени любого положительного числа а с любым положительным рациональным показателем r . Если же показатель r  является рациональным и отрицательным, то выражение а^r определяется как величина, обратная к а^{— r}

       (3)

Здесь  уже  число  — r   положительно. Наконец,  если r = 0,  то а^r   равно  1:

а⁰ = 1.                 (4)

Формулы (1), (2), (3) и (4) определяют степень положительного   числа   а   для любого рационального показателя r.

Для дальнейшего нам  потребуются следующие две теоремы.

Теорема 1. Если число а больше 1 , то из двух степеней этого числа с положительными рациональными показателями больше та, показатель которой больше.

Доказательство. Пусть a > 1   и ^m/_n > ^p/_q,   где  т,  п, р и q  — натуральные числа.  Покажем,  что

Действительно,

Приведем эти корни к корням с одинаковыми показателями:

Так как ^m/_n > ^p/_q , то mq > пр. Поскольку   а > 1, то отсюда вытекает, что а^mq  > а^np  а потому и  ^nq√а ^mq     > ^nq√а ^np     или

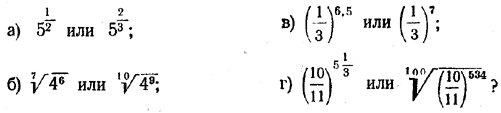
Аналогично может быть доказана и другая теорема.

Теорема 2. Если число а больше нуля, но меньше 1, то из двух степеней этого числа с положительными рациональными показателями больше та, показатель которой меньше.

Доказательство этой теоремы предлагаем учащимся провести самостоятельно.

Примеры.    1)   1,4 <. 1,5.  Поэтому

3^1,4 < 3^1,5

^{(  1}/₃ ^{) 1,4  >  (  1}/₃ ^{) 1,5}

2) 0,51 < 0,52.   Поэтому

π^0,51 <  π^0,52  ;

^{(  π}/₄ ^{) 0,51  >  (  π}/₄ ^{) 0,52}

1358.  Какое число больше:

ОТВЕТЫ