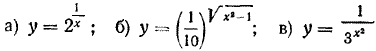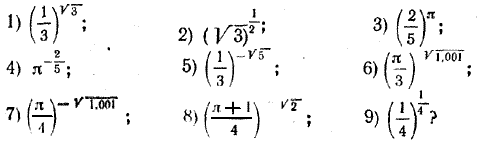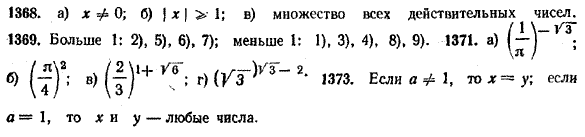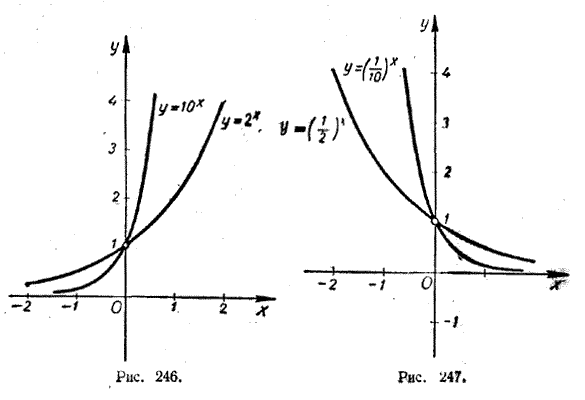
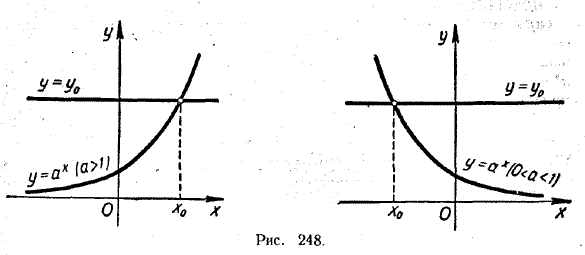
Сборник задач по алгебре.

ПОКАЗАТЕЛЬНАЯ И ЛОГАРИФМИЧЕСКАЯ ФУНКЦИИ VIII

§ 179 Основные свойства показательной функции

В этом параграфе мы изучим основные свойства показательной функции

у = а^x (1)

Напомним, что под а в формуле (1) мы подразумеваем любое фиксированное положительное число, отличное от 1.

Свойство 1. Областью определения показательной функции является совокупность всех действительных чисел.

В самом деле, при положительном а выражение а^x определено для любого действительного числа х.

Свойство 2. Показательная функция принимает только положительные значения.

Действительно, если х > 0, то, как было доказано в § 176,

а^x> 0.

Если же х <. 0, то

а^x=

где — х уже больше нуля. Поэтому а^—^x > 0. Но тогда и

а^x= > 0.

Наконец, при х = 0

а^x = 1.

2-е свойство показательной функции имеет простое графическое истолкование. Оно заключается в том, что график этой функции (см. рис. 246 и 247) располагается целиком выше оси абсцисс.

Свойство 3. Если а >1, то при х > 0 а^x > 1, а при х < 0 а^x< 1. Если же а < 1, то, наоборот, при х > 0 а^x< 1, а при х < 0 а^x > 1.

Это свойство показательной функции также допускает простую геометрическую интерпретацию. При а > 1 (рис. 246) кривые у = а^x располагаются выше прямой у = 1 при х > 0 и ниже прямой у = 1 при х < 0.

Если же а < 1 (рис. 247), то, наоборот, кривые у = а^x располагаются ниже прямой у = 1 при х > 0 и выше этой прямой при х < 0.

Приведем строгое доказательство 3-го свойства. Пусть а > 1 и х — произвольное положительное число. Покажем, что

а^x > 1.

Если число х рационально (х = ^m/_n) , то а^x = а ^{m /}n = ⁿ√a^m .

Поскольку а > 1, то и а^m> 1, Но корень из числа, большего единицы, очевидно, также больше 1.

Если х иррационально, то существуют положительные рациональные числа х' и х", которые служат десятичными приближениями числа x :

х' < х < х".

Но тогда по определению степени с иррациональным показателем

а^x' < а^x < а^x'' .

Как показано выше, число а^x' больше единицы. Поэтому и число а^x, большее, чем а^x', также должно быть больше 1,

Итак, мы показали, что при a >1 и произвольном положительном х

а^x> 1.

Если бы число х было отрицательным, то мы имели бы

а^x=

где число —х было бы уже положительным. Поэтому а^—^x > 1. Следовательно,

а^x = < 1.

Таким образом, при а > 1 и произвольном отрицательном x

а^x < 1.

Случай, когда 0 < а < 1, легко сводится к уже рассмотренному случаю. Учащимся предлагается убедиться в этом самостоятельно.

Свойство 4. Если х = 0, то независимо от а а^x =1.

Это вытекает из определения нулевой степени; нулевая степень любого числа, отличного от нуля, равна 1. Графически это свойство выражается в том, что при любом а кривая у = а^x (см. рис. 246 и 247) пересекает ось у в точке с ординатой 1.

Свойство 5. При а >1 показательная функция у = а^x является монотонно возрастающей, а при а < 1 — монотонно убывающей.

Это свойство также допускает простую геометрическую интерпретацию.

При а > 1 (рис. 246) кривая у = а^x с ростом х поднимается все выше и выше, а при а < 1 (рис. 247) — опускается все ниже и ниже.

Приведем строгое доказательство 5-гo свойства.

Пусть а > 1 и х₂ > х₁. Покажем, что

а^x²> а^x¹

Поскольку х₂ > х₁., то х₂ = х₁ + d, где d —некоторое положительное число. Поэтому

а^x² — а^x¹ = а^x^{1+ d}— а^x¹ = а^x¹ (а^d — 1)

По 2-му свойству показательной функции а^x¹ > 0. Так как d > 0, то по 3-му свойству показательной функции а^d > 1. Оба множителя в произведении а^x¹ (а^d — 1) положительны, поэтому и само это произведение положительно. Значит, а^x² — а^x¹ > 0, или а^x²> а^x¹, что и требовалось доказать.

Итак, при a > 1 функция у = а^x является монотонно возрастающей. Аналогично доказывается, что при а < 1 функция у = а^x является монотонно убывающей.

Следствие. Если две степени одного и того же положительного числа, отличного от 1, равны, то равны и их показатели.

Другими словами, если

а^b = а^c (а > 0 и а =/= 1),

то

b = с.

Действительно, если бы числа b и с были не равны, то в силу монотонности функции у = а^x большему из них соответствовало бы при а >1 большее, а при а < 1 меньшее значение этой функции. Таким образом, было бы или а^b > а^c, или а^b < а^c. И то и другое противоречит условию а^b = а^c. Остается признать, что b = с.

Свойство 6. Если а > 1, то при неограниченном возрастании аргумента х (х —> ∞) значения функции у = а^x также неограниченно растут (у —> ∞). При неограниченном убывании аргумента х (х —> —∞) значения этой функции стремятся к нулю, оставаясь при этом положительными (у—>0; у > 0).

Принимая во внимание доказанную выше монотонность функции у = а^x , можно сказать, что в рассматриваемом случае функция у = а^x монотонно возрастает от 0 до ∞.

Если 0 < а < 1, то при неограниченном возрастании аргумента х (х —> ∞) значения функции у = а^x стремятся к нулю, оставаясь при этом положительными (у—>0; у > 0). При неограниченном убывании аргумента х (х —> —∞) значения этой функции неограниченно растут (у —> ∞).

В силу монотонности функции у = а^x можно сказать, что в этом случае функция у = а^x монотонно убывает от ∞ до 0.

6-е свойство показательной функции наглядно отражено на рисунках 246 и 247. Строго доказывать его мы не будем.

Нам осталось лишь установить область изменения показательной функции у = а^x (а > 0, а =/= 1).

Выше мы доказали, что функция у = а^x принимает только положительные значения и либо монотонно возрастает от 0 до ∞ (при а > 1), либо монотонно убывает от ∞ до 0 (при 0 < а <. 1). Однако остался невыясненным следующий вопрос: не претерпевает ли функция у = а^x при своем изменении каких-нибудь скачков? Любые ли положительные значения она принимает? Вопрос этот решается положительно. Ecли а > 0 и а =/= 1, то, каково бы ни было положительное число у₀обязательно найдется х₀, такое, что

а^x⁰ = у₀.

(В силу монотонности функции у = а^x указанное значение х₀будет, конечно, единственным.)

Доказательство этого факта выходит за пределы нашей программы. Геометрическая интерпретация его состоит в том, что при любом положительном значении у₀ график функции у = а^x обязательно пересечется с прямой у = у₀ и притом лишь в одной точке (рис. 248).